Uso de variogramas en el muestreo de plantas

El siguiente artículo tiene como propósito difundir el uso de esta herramienta para su aplicación en los procesos de planta para materiales particulados, a granel y líquidos.

Un variograma (más precisamente “semivariograma”) es un gráfico de las diferencias promedios de una característica de calidad, entre pares de unidades seleccionadas como función del tiempo o distancia, donde los pares son escogidos de múltiplos de números enteros (por ejemplo, cada metro, 2m, 3m, etc. o cada segundo, 2s, 3s, etc.[2]. A estas distancias también se les denomina lag o rezagos. 

Su propósito es identificar la presencia de tendencias y ciclos en la variación de calidad, evaluar la periodicidad de esos ciclos, y determinar la frecuencia de muestreo apropiada en un proceso de una planta minera o industrial [1].

La siguiente tabla presenta un ejemplo de cómo se construyen estos lag de los resultados obtenidos sobre incrementos tomados cada 2 minutos:

Esquemáticamente se puede representar de esta forma:

A partir de los lag obtenidos del experimento variográfico podemos determinar las siguientes varianzas, que se les denomina semivariogramas (porque las varianzas están divididas por 2): 

semivariograma absoluto:

semivariograma relativo:

donde:

V(j) es la varianza en el j-ésimo lag;

Nu es el número de pares de incrementos en la unidad U (término constante);

j: es el número del lag;

a_L es el contenido de interés promedio en el lote L (término constante);

a es el contenido de interés en un incremento dado;

a_m es el m-ésimo resultado del contenido de interés correspondiente al lag j ;

a_m+j es el (m+j)-ésimo resultado del contenido de interés correspondiente al lag j.

Errores del proceso en planta para materiales particulados

Según la teoría de Pierre Gy, existen tres tipos de errores asociados al proceso de planta que pueden ser tratados con el semivariograma:

1. Error de corto plazo; fluctuación aleatoria de la calidad (discontinuo).- Este error refleja la naturaleza aleatoria de la heterogeneidad de constitución dentro de una unidad o un incremento. Para líquidos puros, sin partículas en suspensión, estas fluctuaciones se pueden considerar despreciables, pero no nulas.
2. Error de largo plazo fluctuación no aleatoria de la calidad.- Este error es principalmente continuo, representa las tendencias entre unidades. También podría ser definido como la segregación a largo plazo o como una regionalización desde el punto de vista de la geoestadística.

3. Error de fluctuación periódica (cíclica) de la calidad.- Este error es continuo y no aleatorio, los ciclos pueden ser introducidos por operaciones de recuperación o acciones correctivas para mantener un parámetro entre dos límites conocidos. Tales ciclos son detrimentales a la calida

Componentes del semivariograma

Componente V[j=0].- Es un término discontinuo, aleatorio y de muy corto plazo que representa la variabilidad inherente de los datos de la muestra. En materiales rocosos mineralizados con metales preciosos, ésta corresponde a la presencia de granos grandes de pepita o de agrupaciones de granos pequeños. En los flujos de procesos, ésta corresponde a la variabilidad aleatoria de corto plazo V[0] , la cual depende directamente del error fundamental (FE), del error de segregación y agrupamiento (GSE) y de otro errores espúreos o no contabilizados. Comúnmente, se le conoce como "Efecto nugget".
La intersección del variograma con el eje y nos da el valor V[j=0]. Este valor es válido y por ende la extrapolación, siempre y cuando el valor de j = 1 sea pequeño, es decir en intervalos de segundos o pocos minutos. Con esto el valor de j=1 probablemente incluya solamente la variabilidad aleatoria.

Componente Sill (meseta).- Es una medida de la variabilidad total en el sistema. Corresponde al conjunto de datos más allá del punto donde las muestras están correlacionadas entre sí.
En otras palabras, cuando la curva se torna horizontal, o sea se alcanza el sill (umbral), ya no se aprecia correlación entre ellas.

Rango de influencia.-  Es el punto más allá del cual ya no hay correlación entre los puntos de datos.

Las flechas rojas indican la zona de covarianzas o de correlación (w₁, w₂, w₃).

Funciones auxiliares del semivariograma

Existen 3 funciones que son complementarias a las anteriores:

1. Integral promedio de primer orden, w
2. Integral promedio de segundo orden w´
3. Media móvil

Estas tienen por objeto:

• Extrapolar el semivariograma a V(0) con gran precisión y exactitud;
• Suavizar la variabilidad residual aleatoria;
• Suavizar la variabilidad cíclica;
• Calcular la varianza s²(HFE) del error total de fluctuación de la heterogeneidad y sus componentes;
• Controlar el proceso de una mejor forma poniendo el foco en la variabilidad relevante;
• Predecir el desempeño de una operación de mezclado.

Definición del generador de error

Un generador de error, E(j), se define como una función del intervalo variográfico j, que se deriva del semivariograma y sus funciones auxiliares, y que a menudo se reduce a una constante que se puede dividir por el numero de incrementos Q, para constituir una muestra S, el cual sirve para calcular la varianza s²(HFE) del error de fluctuación de heterogeneidad continua, HFE.

A continuación, se muestran los cálculos del error de fluctuación de la heterogeneidad, HFE, a partir de los E(j) para distintos tipos de muestreo:

1.- Para el muestreo sistemático:

               donde E(j)_sy es un error generado por el muestreo sistemático:

E(j)_sy = 2W(j/2) - W´(j)

2.- Para el muestreo aleatorio estratificado:

               donde E(j)_st es un error generado por el muestreo aleatorio estratificado:

E(j)_st = W´(j)

3.- Para el muestreo estrictamente aleatorio:

               donde E(j)_ra es un error generado por el muestreo estrictamente aleatorio:

Determinación del intervalo de muestreo:

Para determinar el intervalo de muestreo, se deben calcular previamente los siguientes términos.
a) cálculo punto a punto de la integral promedio de primer orden, w:

donde, para j > 0:

y para j = 0:

S(0) = 0

b) cálculo punto a punto de la integral promedio de segundo orden, w´:

donde, para j > 0:

y para j = 0:

S´(0) = S(0) = 0

Consideraciones importantes para el experimento variográfico

Tomar no menos de 25 muestras
El número de pares Nu - j para el análisis variográfico debe ser menor a Nu/2.
Para determinar V(0) tomar en cuenta que los intervalos sean segundos o hasta pocos minutos,

Ejemplo de determinación del intervalo de muestreo

En el siguiente ejemplo, se quiere determinar el error de muestreo para una operación de planta donde se toma una muestra cada 8 horas, con incrementos extraídos cada 20 minutos y determinar los errores de muestreo a distintos intervalos de tiempo.

Lo primero que debemos hacer, es calcular el término V(0) que corresponde al error de corto plazo. Para determinar V(0), nos conviene realizar un experimento variográfico por separado, ya que necesitamos intervalos de segundos o pocos minutos para que esta componente incluya solamente la variabilidad aleatoria.

Por lo tanto, este primer experimento considerará tomar unas 60 muestras a intervalos de 20 seg.

Resultados:

Los resultados del semivariograma relativo se muestran a continuación en la siguiente tabla:

Con esta información se obtiene el siguiente semivariograma:

Con esto calculamos V(0).

V(0) = 1,70 x 10^-04

Ahora bien, para determinar V(j) a largo plazo, realizamos el experimento variográfico tomando 80 muestras cada 10 min.
A continuación, se presentan los resultados:

Los resultados del semivariograma relativo se muestran a continuación en la siguiente tabla, considerando el V(0) obtenido en el experimento anterior: 

(NOTA.- TABLA CORREGIDA JULIO 2021)

Algunos cálculos importantes:

Para obtener V(0) con 2 puntos:
Extrapolación con V(0)
V(0) = 2*V(1)-V(2)

Extrapolación con W(0)

V(0) = 2*W(1) - W(2)

Para obtener S(j):


S(0) = 0
S(1) = S(0) + V(0)/2 + V(1)/2
S(2) = S(1) + V(1)/2 + V(2)/2
...

Para obtener W(j):

W(0) = V(0)
W(1) = (1/1)*S(1)
W(2) = (1/2)*S(2)
...

Para obtener S´(j):

S´(0) = 0
S´(1) = S´(0) + S(0)/2 + S(1)/2
S´(2) = S´(1) + S(1)/2 + S(2)/2
...

Para obtener W´(j):

W´(0) = V(0)
W´(1) = [2/(1^2)]*S´(1)
W´(2) = [2/(2^2)]*S´(2)
...

Para obtener 2W(j/2):
Se parte de:

Si j es impar:
j = 2j₀ +1
j₀ =(j - 1)/2
2W(j/2) = W(j₀) + W(j₀+1)

Si j es par:
j=2j₀
j₀ = j/2
2W(j/2) = 2W(j₀)

Así:
Para j = 1    ;   j₀ = (1-1)/2 = 0  ;    2W(j/2) = W(0) + W(1)
Para j = 3     ;  j₀ = (3-1)/2 = 1   ;   2W(j/2) = W(1) + W(2)
Para j = 5     ;  j₀ = (5-1)/2 = 2   ;   2W(j/2) = W(2) + W(3)
....

Para j = 2    ;  j0 = 2/2 = 1          ;  2W(j/2) = 2W(1)
Para j = 4    ;  j0 = 4/2 = 2          ;  2W(j/2) = 2W(2)
Para j = 6    ;  j0 = 6/2 = 3          ;  2W(j/2) = 2W(3)
....

Para obtener E(j)_sy para muestreo sistemático:
E(j)_sy = 2W(j/2) - W´(j)

Para j = 1 ; E(1)_sy = W(0)+W(1) - W´(1)
Para j = 2 ; E(2)_sy = 2W(1) - W´(2)
Para j = 3 : E(3)_sy = W(1)+W(2) - W´(3)
Para j = 4 ; E(4)_sy = 2W(2) - W´(4)
Para j = 5 : E(3)_sy = W(2)+W(3) - W´(5)
Para j = 6 ; E(4)_sy = 2W(3) - W´(6)
....

Semivariograma relativo para el segundo experimento variográfico:

Determinación del error de muestreo de planta:

s²(HFE)_sy = E(j)sy/Q

La planta tiene un intervalo cada 20 min, que equivale al lag 2 (j =2) del segundo experimento variográfico.  Considerando que se toman las muestras cada 8 horas, el número de incrementos para cada intervalo es:

Q = (60/ x)*8
donde x es el intervalo de tiempo.

Para j = 1  ;  10 min ;  Q = (60/10)*8 = 48 incrementos
Para j = 2  ;  20 min ;  Q = (60/20)*8 = 24 incrementos
Para j = 3  ;  30 min ;  Q = (60/30)*8 = 16 incrementos
....

Para un muestreo sistemático con j = 2:
S²(HFE)_sy = [2W(1) - W´(2)] / 24 = 0,000329/ 24 = 1,369 x 10^-5

Por lo tanto, la desviación estándar relativa para el error de fluctuación de la heterogeneidad continua de esta planta, para esa configuración de muestreo (incrementos cada 20 min y toma de muestra cada 8 horas) es:

s(HFE)_sy = 0,37%

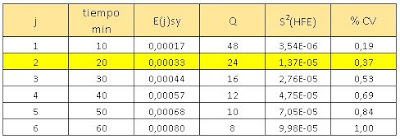
A continuación, los errores de muestreo calculados para distintos intervalos: 

(NOTA.- TABLA CORREGIDA JULIO 2021)

Nota.- s(HFE)_sy = RSD = CV 

Sobre la teoría de Pierre Gy visitar mi otro post: Teoría de Pierre Gy

Referencias

[1] Smith P. "A primer for sampling for solid, liquid and gases. Based on the seven sampling errors of Pierre Gy. Ed 2001.
[2] Pitard F.F. "Theory of sampling and sampling practice. 3° Ed. 2019. CRC Press.
[3] Minnit R.C.A., Pitard F. "Application of variography to the control of species in material process streams: %Fe en un producto de mineral de hierro". The Journal of The Southern African Institute of Mining and Metallurgy, vol 108. Ed 2008.

[4] Gy Pierre - "Sampling of heterogeneous and dynamic material systems". Ed 1992.
[5] Gy Pierre - "Sampling particulates material - Theory and practice". Ed. 1979.
[6] Gaetan C., Guyon X. "Spatial Statistics and modelling". Ed. 2010. 

Pincha aquí para saber más acerca de los cursos que se ofrecen en 2023: CURSOS ONLINE