El error asociado a los algoritmos en Absorción Atómica y el Error fotométrico

Introducción

El siguiente artículo tiene por objeto presentar la cuantificación del error asociado al ajuste de los algoritmos de absorción atómica del equipo Varian obtenidos experimentalmente en el laboratorio, utilizando el elemento cobre en la línea principal 324,8 nm y en la curva extendida hasta 0,9  ua. También mostrar un método para determinar el error fotométrico de acuerdo a los criterios señalados por el paper de A. Ringbom que pueden ser de utilidad en la validación de las metodologías analíticas.

Análisis del error asociado a los algoritmos de Absorción atómica (Varian)

Para ello, se prepararon 10 soluciones de muestras cuyas concentraciones de cobre van desde los 0,0 a los 8,0 mg/L. Luego se ajustó la sensibilidad del equipo de acuerdo a las especificaciones del fabricante a esa longitud de onda; 1,5 mg/L = 0,200 ua., obteniéndose resultados en absorbancias hasta aprox. 0,900 u.a,

Los resultados que se muestran en la tabla siguiente se analizaron aplicando los siguientes algoritmos; lineal, lineal origen, cuadrático, cuadrático origen y nuevo racional. 

Los siguientes fueron los resultados:

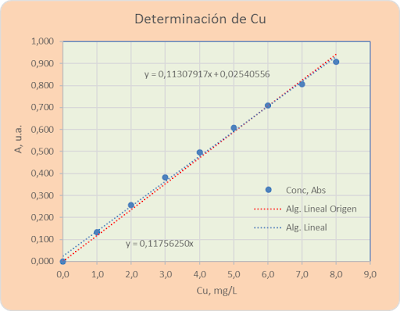
Algoritmo Lineal y Lineal Origen

				Alg. Lineal		Alg. Lineal Origen
Conc Cu  mg/L	Abs 1 u.a.	Abs 2 u.a.	Abs prom u.a.	C lin mg/L	|Er| % sesgo	C lin o. mg/L	|Er| % sesgo
0,0	0,0000	0,0001		-0,22		0,00
1,0	0,1313	0,1356	0,1335	0,96	4,5	1,14	13,5
2,0	0,2566	0,2560	0,2563	2,04	2,1	2,18	9,0
3,0	0,3789	0,3853	0,3821	3,15	5,1	3,25	8,3
4,0	0,4932	0,4969	0,4951	4,15	3,8	4,21	5,3
5,0	0,5965	0,6200	0,6083	5,15	3,1	5,17	3,5
6,0	0,7088	0,7099	0,7094	6,05	0,8	6,03	0,6
7,0	0,8120	0,8015	0,8068	6,91	1,3	6,86	2,0
8,0	0,9074	0,9090	0,9082	7,81	2,4	7,73	3,4

Gráficas asociadas:

Conclusión.- De acuerdo a los resultados obtenidos se puede concluir que para la curva de cobre en el rango de trabajo hasta 0,9 u.a. el algoritmo lineal presenta mayor sesgo principalmente en el centro de la recta y en los extremos como era esperable debido a la curvatura que presentan los datos. 

Lo mismo ocurre con el algoritmo lineal origen. Sin embargo, el error aumenta en forma significativa respecto al algoritmo lineal, siendo más grande en los niveles cercanos al ajuste (concentraciones bajas). Los valores obtenidos son significativos y demuestra que no deben utilizarse este tipo de algoritmo si se utiliza todo el rango de absorbancia señalado.

Algoritmo Cuadrático y Cuadrático Origen

				Alg. Cuadrático		Alg. Cuadrático Origen
Conc Cu  mg/L	Abs 1 u.a.	Abs 2 u.a.	Abs prom u.a.	C cua mg/L	|Er| % sesgo	C cua o. mg/L	|Er| % sesgo
0,0	0,0000	0,0001		0,00		0,00
1,0	0,1313	0,1356	0,1335	1,01	0,9	1,01	1,4
2,0	0,2566	0,2560	0,2563	1,98	0,9	1,99	0,7
3,0	0,3789	0,3853	0,3821	3,02	0,7	3,03	0,9
4,0	0,4932	0,4969	0,4951	4,00	0,1	4,00	0,1
5,0	0,5965	0,6200	0,6083	5,02	0,5	5,03	0,6
6,0	0,7088	0,7099	0,7094	5,98	0,3	5,99	0,2
7,0	0,8120	0,8015	0,8068	6,96	0,6	6,97	0,5
8,0	0,9074	0,9090	0,9082	8,03	0,4	8,04	0,5

Conclusión.- Los algoritmos cuadráticos corrigen bastante bien respecto a los algoritmos anteriores y las diferencias son bastante aceptables, no superando el 1% sobre aprox. 0,250 u.a.

Algoritmo Nuevo Racional

				Alg. Nuevo Racional
Conc Cu  mg/L	Abs 1 u.a.	Abs 2 u.a.	Abs prom u.a.	C n. rac. mg/L	|Er| % sesgo
0,0	0,0000	0,0001
1,0	0,1313	0,1356	0,1335	1,01	0,5
2,0	0,2566	0,2560	0,2563	1,98	1,2
3,0	0,3789	0,3853	0,3821	3,02	0,6
4,0	0,4932	0,4969	0,4951	4,00	0,0
5,0	0,5965	0,6200	0,6083	5,03	0,6
6,0	0,7088	0,7099	0,7094	5,99	0,1
7,0	0,8120	0,8015	0,8068	6,96	0,5
8,0	0,9074	0,9090	0,9082	8,02	0,2

Conclusión.- El algoritmo racional se comporta un poco mejor que los cuadráticos, siendo el error ligeramente más bajo, inferior al 1% en casi toda la curva.

Nota.- La idea es construir curvas de calibración dentro del rango de ocurrencia de las muestras. En este ejemplo se supone que las concentraciones recurrentes van desde aprox. 1,0 a menos de 8,0 mg/L de Cu.

El error Fotométrico

El error fotométrico corresponde a aquella región donde el instrumento no entrega una respuesta satisfactoria de absorbancia. Eso ocurre cuando pasa demasiada señal al fotodetector y este se satura o cuando la señal que llega al fotodetector es tan baja que prácticamente esta no es detectada.

Se prepararon varias soluciones del elemento cobre hasta 500 mg/L. Se utilizó la longitud de onda = 327,4 nm y la sensibilidad se ajustó a 10 mg/L = 0,130 u.a.

La siguiente tabla entrega los resultados de esta experiencia.

Con esta información se construyeron las gráficas de Crawford y Ringbom que son las que nos sirven para determinar el error fotométrico:

Nota.- dC/C es el error relativo de la concentración y que se coloca a menudo en el eje y del gráfico de Crawford. En este caso se ha graficado dC/C/dT, que corresponde al error analítico por unidad de error fotométrico.

Para obtener el rango donde el instrumento presenta el error mínimo se traza una línea recta que pase por todos los puntos coincidentes en el medio del gráfico. La zona lineal corresponde al intervalo de concentraciones donde el error es mínimo, dC/C por lectura.

Conclusión.- El error fotométrico se incrementa significativamente por debajo de 0,065 u.a. y por sobre 1,149 u.a.

Obtención de la expresión dC/C

dC/C representa el error relativo de la concentración, y este se grafica vs la transmitancia para obtener el gráfico de Crawford.

Partimos de la base que:

A = abc
A = -logT

expresiones que corresponden a la ley de Lambert-Beer.
Por lo tanto:

-logT = abc
logT = -abc

Si elevamos a 10 ambos términos, obtenemos:
10^(logT) = 10^(-abc)
T = 10^(-abc)

Luego, derivamos respecto a C:
dT/dC = d (10^(-abc))/dC

Obtenemos:
dT/dC = 10^(-abc) * ln 10 * (-ab)
dT/dC = 2,303 T (-ab)

Invertimos ambos términos para conseguir expresar dC/dT:
dC/dT = 0,4343/T(-ab)

dC = 0,4343dT /T(-ab)

multiplicamos ambos téminos por 1/C:
dC/C = 0,4343dT/T(-ab)c

Como el término -abc = logT, reemplazamos:
dC/C = 0,4343dT/TlogT

que es finalmente la expresión que nos interesaba llegar.
dC/C es el error relativo y con esto graficamos vs T% para obtener la curva de Crawford.

Nota.- De esta expresión también podemos conocer cual es la sensibilidad limite en espectroscopía, el cual corresponde a aprox. al 1% de la señal de absorción:

     Lim      A = 0,0044

  E → 100%    

donde E corresponde al error analítico por unidad de error fotométrico que es:
E = (dC/C)/dT      

Referencias
1.- A. Ringbom, Z. Anal.Chem. 115 (1939) 333.
2.- B..E. Limbeck & C.J. Rowe, "Curve Correction in Atomic Absorption", Agilent Technologies, 1986.
3.- Handbook Flame analytical Methods of Varian
4.- Curso de "Validación de Metodologías Analíticas" de Mauricio Arancibia G

Pincha aquí para saber más acerca de los cursos que se ofrecen en 2023: CURSOS ONLINE