El control de calidad de los laboratorios, tanto externos como internos, resulta vital para asegurar los resultados analíticos con las cuales se deben tomar decisiones respecto de sus procesos.
Uno de esos controles y del cual es el objetivo del presente artículo es el control de la variabilidad de los resultados.
Esta variabilidad puede medirse de diversas maneras y utilizando diferentes estadísticos (rango, desviación estándar, varianza, error relativo, coeficiente de variación, varianza relativa, etc.)
Howarth y Thompson en 1973 propusieron el siguiente esquema de trabajo para controlar la precisión de los laboratorios, donde la precisión se expresa mediante el coeficiente de variación, también conocido como desviación estándar relativa (RSD en inglés).
Construcción del estadístico de Howarth-Thompson
El estadístico de Howarth - Thompson está desarrollado para análisis en duplicados. Y en base al trabajo desarrollado por estos autores, se llegó a obtener una curva de precisión que es una hipérbola de forma:
Ahora bien, el Coeficiente de variación, por definición corresponde a:
CV = s/c (1.1)
La precisión expresada con un nivel de probabilidad del 95 % es:
CV = 2s/c (1.2)
Otra forma de denotarlo es:
P =
Precisión, expresada como coeficiente de variación porcentual (CV%) con un nivel de probabilidad del 95%.
s = desviación estándarc = concentración media entre duplicados
La desviación estándar, s, que es función de la
concentración se estima a partir de la Mediana de las diferencias absolutas (abs diff) entre duplicados cada 11 muestras.
Pero la desviación estándar de la concentración es:
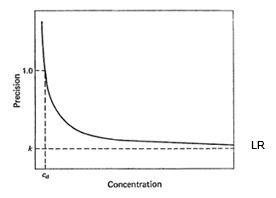
Sc = kc + S0 (1.4)
que se desprende de la curva de regresión del siguiente gráfico.
k es la pendiente de la curva de regresión y S0 es es el intercepto.
Por lo tanto, despejando (1.4) en (1.3), tenemos:
Procedimiento de validaciónSc = kc + S0 (1.4)
que se desprende de la curva de regresión del siguiente gráfico.
k es la pendiente de la curva de regresión y S0 es es el intercepto.
Por lo tanto, despejando (1.4) en (1.3), tenemos:
que corresponde al estadístico de precisión Howarth-Thompson
Una forma equivalente de expresar este estadístico, pero expresado con un nivel de probabilidad del 99,73% es:
Pc = 3So/c + LR (1.7)
donde LR es el límite de repetibilidad que es igual a:
LR = 3K (1.8)
Para N > 50 duplicados
a) Los duplicados se ordenan de menor a mayor
b) Se calcula la media y las diferencias absolutas de cada uno
c) Se calculan las media de las medias y las medianas de las diferencias absolutas cada 11 duplicados.
d) Se calcula la pendiente, m, y el intercepto, s0.
e) Se calcula el límite de detección de acuerdo a la siguiente expresión:
f) Se calcula el Estadístico de H-T, Pc, de acuerdo a la expresión (1.6) o (1.5)
g) Se borran todos los datos bajo el límite de detección.
h) Se grafica este estadístico, Pc vs la concentración.
Esta curva corresponde a línea de control de la precisión estimada con un nivel de probabilidad del 95%
Procedimiento de Control de calidad mediante el estadístico H-T para muestras en duplicados (corregido)
Una vez realizada la validación, se efectúa el control de calidad de las muestras en duplicados en la cual se pueden considerar las siguientes expresiones:
la cual corresponde a la mitad del error relativo.
A continuación, se muestra un ejemplo de este criterio:
Aquí se puede apreciar que el criterio HARD es menos exigente.
Los mismos datos, pero graficados en Excel usando el criterio HARD.
Fuente:
[1] Michael Thompson y Richard J. Howarth.
The Rapid Estimation and Control of Precision by Duplicate Determination. The Analist,
Marzo
de 1973.
[2] Michael Thompson y Richard J. Howarth. Duplicate Analysis in Geochemical Practice - Part 1. Theoretical Approach and Estimation of Analytical Reproducibility. Awalyst, September, 1976, Vol. 101, pp. 690-698
[3] Marat Abzalov (2011). Sampling Errors and Control of Assay Data Quality in Exploration and Mining Geology, Applications and Experiences of Quality Control, Prof. Ognyan Ivanov (Ed.), ISBN: 978-953-307-236-4
[4] Bumstead, E.D. (1984). Some comments on the precision and accuracy of gold analysis exploration. Proceedings AusIMM, No. 289, p.71-78, ISSN 1034-6783
Pincha aquí para saber más acerca de los cursos que se ofrecen en 2023: CURSOS ONLINE











Excelente herramienta. Muy bien explicado. Muchas gracias
ResponderEliminar