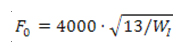El siguiente artículo trata del procedimiento que fue establecido por F. Bond para obtener las dimensiones de un molino de bolas ideal.
A partir de la llamada tercera ley de
la conminución, Fred Bond desarrolló un procedimiento para estimar las
dimensiones de varios equipos industriales, entre los que se incluye el “molino
de bolas”.
Este procedimiento si bien tiene un
error de estimación cercana al ±20 %, continúa aun siendo utilizado en la
actualidad debido a la gran simplicidad en sus cálculos.
Procedimiento
1.-Determinación del WI
del material a través de pruebas estándar de laboratorio.
2.- El valor del WI
calculado es para un molino de bolas en condiciones estándar, es decir,
considerando tipo descarga por rebalse, de 8 pies de diámetro interior,
molienda en húmedo y en circuito cerrado. Este valor se conoce como Valor base
de WI.
3.- En caso que estas condiciones no
se cumplan, se deberán considerar los siguientes factores de corrección:
Factor f1 ; molienda en
seco
Factor f2 ; molienda en
circuito abierto
Factor f3 ; factor
eficiencia por diámetro del molino
Factor f4 ; alimentación
demasiado gruesa
Factor f5 ; sobremolienda
de finos, obteniéndose P80 ≤ 75µm
Factor f6 ; baja razón de
reducción en el molino
Si el factor no tiene influencia
entonces, el factor es igual a 1.
donde:
WI (corr): Work index corregido
Factor f1 : Para el
mismo rango de trabajo de molienda húmeda, F. Bond estimó que la molienda seca
requiere 1,3 veces más potencia que la molienda húmeda. Es decir f1
= 1,3.
Factor f2 : En circuito
abierto, la molienda húmeda requiere una cantidad extra de potencia si se le
compara cuando se efectúa en circuito cerrado. El valor del factor depende del
producto de molienda producido y su valor se entrega en la siguiente tabla:
Tamaño de Control del Producto Factor
(Referencia a % pasante) f2
50 1,035
60 1,050
70 1,100
80 1,200
90 1,400
92 1,460
95 1,570
98 1,700
Factor f3 : El diámetro
interno del molino afecta la eficiencia de molienda. Para condiciones no
estándar, es decir, D ≠ 8
pies , el factor f3 está dado por:
donde:
D: diámetro
interno del molino en pies, medido entre revestimientos.
En operación
de Planta, cuando D ≥ 12,5
pies , la eficiencia llega a un máximo manteniéndose en
un valor constante y f3 = 0,914.
Como D es un
parámetro desconocido al comienzo, F. Bond sugiere considerar f3 =
1, durante la primera iteración cuando D ≠ 8 pies y luego recalcular
dicho valor más adelante.
Factor f4 : Este
factor se utiliza cuando el material con que se alimenta el molino es más
grueso que un cierto valor óptimo. Este factor se relaciona directamente con el
Work Index, según la siguiente ecuación:
Donde:
Rr
: razón de reducción del 80 % = F80/P80
F80
: tamaño 80 % de alimentación (µm)
P80
: tamaño 80 % del producto (µm)
WI : Work Index
del material (KWh/ton. corta)
F0 : tamaño óptimo
de alimentación (µm)
Siendo:
Factor f5 : Cuando hay
una sobremolienda de finos, es decir, el tamaño 80% pasante del producto es
menor que 75 micrones (200 mallas) se aplica el factor f5 de acuerdo
a la siguiente ecuación:
Factor f6 : Cuando la
razón de reducción del molino es baja, es decir menor a 6, se aplica el factor
f6, como ocurre en el proceso de remolienda de concentrados y
relaves de circuitos industriales.
El Work Index corregido está
dado por la siguiente expresión:
El consumo de energía
específica en la molienda industrial, para ir desde un tamaño 80 % pasante F80
hasta un tamaño 80 % pasante P80 está dado por:
Donde:
W : Consumo de energía (KWh)
necesario para reducir una tonelada corta de material, desde un tamaño 80 %
pasante F80 (µm) hasta 80 % pasante P80 (µm).
WI, P80
y F80 corresponden al Work Index (KWh/ton corta), a los tamaños 80 %
pasante del producto final y alimentación fresca del circuito industrial de
molienda (µm).
La potencia mecánica
requerida para la molienda del material está dado por:
O bien:
Donde C : capacidad deseada
del circuito para la conminución del material de molienda / clasificación (TPH
de sólidos procesados), expresado en ton corta/h.
La potencia mecánica
calculada de esta forma es la potencia requerida en el eje piñón del molino, la
cual incluye pérdidas por eficiencia en rodamientos, engranajes y piñón, pero
NO incluye las pérdidas de eficiencia en el motor y otros componentes accesorios,
tales como reductores de velocidad, pérdidas de transmisión, etc.
La potencia eléctrica
requerida en la entrada del motor, suponiendo una eficiencia de h % (normalmente h = 95 %) está dado por:
Donde PE (HP):
Potencia eléctrica requerida en la entrada del motor, medido en HP
PM (HP) : Potencia
mecánica requerida para la conminución del material, medido en HP
A partir de la siguiente
ecuación para calcular el consumo de potencia eléctrica en molino de bolas y
utilizada por algunas empresas de ingeniería,
se determina el valor de D,
una vez especificado los valores de PE (HP), KB, %VP,
%CS y la razón L/D.
Donde:
PE (HP) : Potencia
eléctrica requerida a la entrada del motor (HP)
D : diámetro interno del
molino (pies). Se aconseja D = 20
pies
%VP : % del
volumen interno del molino cargado con bolas (volumen aparente de la carga de
bolas), expresado como porcentaje. Se aconseja utilizar un valor de %VP
entre 40 y 50 %.
%CS : % de
velocidad crítica del molino, expresado como porcentaje. Se aconseja utilizar
un valor entre 68 y 78 % de la velocidad crítica.
L : Longitud interna del
molino (pies). Para la mayoría de los casos prácticos, se puede variar la razón
L/D entre 1 y 3.
KB : Constante de
proporcionalidad, cuyo valor depende del tipo de molino seleccionado, de
acuerdo a la siguiente tabla:
Tipo de molino de bolas
|
Valor de KB
|
|
-
Descarga
por rebalse, molienda húmeda
|
4,365 x 10-5
|
|
-
Descarga
por Diafragma (parrilla), molienda húmeda
|
4,912 x 10-5
|
|
-
Descarga
por Diafragma, molienda seca
|
5,456 x 10-5
|
La ecuación anterior implica hacer una primera estimación de D, la cual se reemplaza en la fórmula (L/D) y se vuelve a calcular iterativamente hasta que el algoritmo de cálculo converja.
Las veces que deberá
repetirse este cálculo, es hasta obtener una variación máxima relativa de 1 %
para valores de D calculados entre iteraciones sucesivas.
Ejemplo Práctico
Se desea reducir un material desde
80% pasante 195(µm), requiriéndose tratar 216tons. Corta hora de sólidos en la
planta de procesamiento;
Los datos conocidos y parámetros por
determinar se resumen a continuación;
WI=14,5 kwh/ton corta.
Molienda en húmedo (65% de sólidos) y
en circuito cerrado.
F80=tamaño 80% alimentación 4763(µm).
P80 =tamaño 80% del producto= 195(µm).
h =eficiencia
del motor=96%.
Molino de Bolas tipo Overflow
(descarga por rebalse).
C=216 ton corta/hora= alimentación
fresca de sólidos al circuito de molienda.
L/D= 1,25 = razón largo/diámetro seleccionada.
%CS =70% de la velocidad crítica.
%VP =45% de carga de bolas (como % del
volumen interno del molino)
Valor de KB =4,63E-5
Solución:
Factor
|
Valor
|
Observaciones
|
f1
|
1.000
|
molienda húmeda
|
f2
|
1.000
|
circuito cerrado
|
f3
|
1.000
|
considerando D=8
c/estimación inicial
|
f4
|
1.079
|
Rr=24,43;Wi=14,5;F₈₀=4763;F₀=3787um
|
f5
|
1.000
|
porque P₈₀>75u.m
|
f6
|
1.006
|
Rr=24,43
|
La siguiente tabla ilustra los cálculos realizados durante cada iteración:
Iteración
|
f3
|
Wi (corr)
|
W;kwh/ton corta
|
PM;HP
|
PE;HP
|
D;pies
|
L;pies
|
%error en D
|
1
|
1
|
15.739
|
8.991
|
2604.18
|
2712.69
|
15.412
|
19.265
|
-
|
2
|
0.915
|
14.402
|
8.226
|
2382.83
|
2482.11
|
15.026
|
18.782
|
2.51
|
3
|
0.915
|
14.402
|
8.226
|
2382.83
|
2482.11
|
15.026
|
18.782
|
0
|
(*)Nota: Como D>12,5 pies ; se supuso f3 =
Cte. =0,915
Por consiguiente, las dimensiones del
molino de bolas serán:
D=15,03 pies, es decir, 15 pies de diámetro
interno.
L=18,78 pies, es decir, 19 pies de longitud
efectiva.
La potencia eléctrica del motor será:
Como en el ejemplo desarrollado, D=15
pies (tamaño relativamente grande para el molino de bolas), se podría pensar
también en la posibilidad de utilizar dos molino de bolas más pequeños operando
en paralelo. En tal caso, cada molino debería consumir una potencia aproximada
de 1300HP, obteniéndose las siguientes dimensiones para cada uno de ellos;
Nº de molinos
de bolas=2
D=12,5 pies de diámetro interno
L=15,5 pies de largo efectivo
PE = 1293 HP / molino que es aprox. 1300 HP en cada molino
Limitaciones y deficiencias de las
teorías clásicas de conminución
Debido a que la metodología desarrollada
por Fred Bond, es la más utilizada en la industria minera para dimensionar
equipos de conminución, a continuación se resumen las principales limitaciones
y deficiencias del método de Bond:
En primer lugar, en el procedimiento
estándar de laboratorio, Bond utiliza un tamiz de separación para simular la
malla de corte obtenida con un clasificador industrial. Es decir se realiza una
“clasificación ideal” del material a escala de laboratorio, lo cual es
imposible de lograr a escala industrial. La mayoría de los clasificadores
industriales poseen características de separación extremadamente variables, con
desviaciones substanciales respecto al comportamiento de separación perfecta.
Segundo, las condiciones de
equilibrio alcanzadas en un test estándar de Bond a escala de laboratorio
corresponden al estado estacionario alcanzado en un molino tipo “plug flow”. Es
decir, está implícito en el método de Bond que los molinos de industriales no
actúan como mezcladores de la pulpa además de moler las partículas del material.
Las características dinámicas de transporte de la pulpa en el molino
normalmente se sitúan entre los casos extremos de mezcla perfecta y
flujo-pistón, de acuerdo a los resultados de numerosos estudios de transporte
de partículas, realizados en molinos industriales.
Tercero, se supone también, en forma
implícita, que todos los tipos de materiales se fracturarán de una manera
similar, es decir, de acuerdo a las características típicas de un “material
ideal tipo Bond”. Dicho material se caracteriza por tener por una distribución granulométrica de
Rosin-Rammmler, con una pendiente igual a 0,5 en la región de tamaños finos.
En la práctica, muy pocos materiales
siguen en forma natural este tipo de distribución, y entre aquellos que así lo
hacen, es muy raro encontrar alguno con pendiente exactamente igual a 0,5.
Cuarto, en el método de Bond se
utilizan sólo 3 parámetros para calcular el consumo de energía en la molienda.
Ellos son: (a) el índice de trabajo (Work Index Wi);(b)un
parámetro de tamaño característico de la alimentación (F₈₀;µm)y(c)un
parámetro de tamaño característico del producto(P₈₀;µm).El
concepto de Work Index, en sí mismo, engloba en un solo parámetro todo el
proceso de fractura, transporte y clasificación del material dentro de un
circuito cerrado de molienda/clasificación. Es por ello que Bond ha debido
incluir una serie de “factores correctores” dentro de su formula básica, a fin
de tomar en cuenta el efecto de diversas variables de operación sobre el
consumo energético de la molienda. Existen correcciones para molienda seca,
circuito abierto, fineza exagerada del producto molido, tamaño de alimentación
demasiado grueso y efecto del diámetro del molino. El objetivo primordial de
estos factores correctores es disminuir las diferencias observadas en planta,
tanto en capacidad como en consumo de potencia, con respecto a los
correspondientes valores determinados mediante la fórmula estándar de Bond.
Debemos recordar, además, que el valor de Wi obtenido a
través del procedimiento estándar de laboratorio ha sido correlacionado con
muchísimos datos experimentales acumulados en planta, a objeto de “calibrar” la
fórmula de escalamiento propuesta por Bond, para calcular el consumo energético
de los materiales molidos de los equipos industriales. Para ello, se ha
utilizado un sinnúmero de resultados experimentales recopilados en planta,
obtenidos fundamentalmente con molinos de 8 pies de diámetro interno,
operando en húmedo, ya sea en circuito cerrado con clasificadores industriales
para molinos de bolas.
Conclusión
El dimensionamiento de los molinos de
bolas mediante factores correctivos de Bond es un método empírico de
correlación, que nos permite determinar una primera estimación de consumo real
de energía para moler un mineral determinado en un molino de tamaño industrial
con un error de ±20%, no obstante, debido a su extrema simplicidad, el
procedimiento de Bond hoy en día aun es utilizado por la industria minera para
dimensionar molinos de bolas a escala piloto, semi-industrial e industrial.
Referencias
- Gutiérrez, L., Sepúlveda, J. 1986. Dimensionamiento y Optimización de Plantas Concentradoras mediante Técnicas de Modelación Matemática. Editado por CIMM, 302 p.
- Artículo de mi autoria.