CÓMO APLICAR LA TEORÍA DE PIERRE GY EN LA PRÁCTICA

El objetivo del muestreo correcto es identificar los errores que se pueden producir en el proceso de muestreo y una vez identificados, cancelarlos o minimizarlos según corresponda. Pero para poder realizar esto, debemos recurrir a la teoría, al modelo que nos facilita este trabajo. En nuestro caso a la teoría de Pierre Gy. 

De esto se trata este artículo, presentar un resumen de la teoría y una estrategia de cómo aplicar esto en la práctica.

Definición del muestreo

Para Pierre Gy, el muestreo corresponde una secuencia de operaciones selectivas y no selectivas que finalizan con la selección de una o diferentes porciones de ensayo del proceso analítico.  

De aquí podemos desprender lo siguiente, el muestreo más que el acto de extraer una fracción de un lote (operación selectiva), es un proceso que involucra además otro tipo de operaciones que él denomina no selectiva en donde podría ocurrir también alteraciones de la integridad del lote y que corresponde a operaciones tales como la carga y descarga del material, traslados, transporte, secado, chancado, pulverizado, almacenamiento, homogenizado, tamizado, ingreso y procesamiento de datos, etc. 

Estrategia para aplicar la teoría de Pierre Gy en la práctica

La siguiente es una estrategia que corresponde a la estrategia implementada por Arech Consultores SpA para minimizar o cancelar según corresponda los diferentes tipos de errores del muestreo que se pueden presentar en un proceso.

Los fenómenos podemos verlos a pequeña escala y a gran escala. Para ver los fenómenos a gran escala, tenemos que alejarnos y ver en su conjunto como por ejemplo los resultados de la planta durante un tiempo determinado. 

A pequeña escala

a) Identificar los tipos de operación en todo el proceso de muestreo

Si partimos de la base de la definición de P Gy, entonces, lo primero que debemos realizar es identificar aquellas operaciones selectivas que tenemos en todo el proceso de muestreo. Y al mismo tiempo, identificar y clasificar por etapas las operaciones de tipo no selectivas del proceso hasta llegar a la porción de ensayo en el laboratorio.

Una vez identificadas cada una de las operaciones (tanto selectivas como no selectivas), podemos partir de un principio, que, si bien no sale de esta forma en el libro de P. Gy, podríamos desprenderla de su definición y que nos va a servir para implementar esta estrategia. Y estos dos principios corresponden a qué es lo que deberíamos considerar para que no se produzcan desviaciones tanto en las operaciones selectivas como en las operaciones no selectivas. 

1.- Principio del muestreo correcto asociado a las operaciones selectivas:

"Todos los constituyentes de interés (también conocidos como características o componentes) del lote deben ser bien representados en la muestra"

2.- Principio del muestreo correcto asociado a las operaciones no selectivas:

"El material no debe sufrir alteración a lo largo de todo proceso de muestreo que afecten los resultados. Que en todo el proceso de muestreo se mantenga las características del lote original (Integridad del lote)"

Nota. - Para cumplir con estos dos principios del muestreo correcto, se deben respetar las 4 reglas del muestreo correcto de Pierre Gy.

1. Todos los fragmentos o grupos de fragmentos deben tener la misma oportunidad de formar parte de la muestra (El no hacerlo provoca el error de delimitación de los incrementos, ED).

2. La herramienta de muestreo no debe volverse selectiva en lo que está tomando (sí lo hace provoca el error de extracción de los incrementos, EE).

3. La masa de los incrementos recolectados debe ser proporcional a la cantidad de material presentado a la herramienta de muestreo (Si no es proporcional se provoca el error de ponderación de los incrementos, EW).

4. La integridad de los incrementos no debe ser alterada bajo ninguna circunstancia (si se altera se provoca el error de preparación de los incrementos, EP).

Las 3 primeras reglas están asociadas a las operaciones selectivas y la cuarta regla a las operaciones no selectivas. Sin embargo, cada vez que realicemos una operación selectiva, para que se cumple el primer principio del muestreo correcto, es decir para que todos los constituyentes de interés sean bien representados en la muestra, en muchos casos vamos a tener que disminuir el tamaño de partícula o aumentar la masa para que la muestra obtenida sea representativa del lote.

Por lo tanto, es importante distinguir entre "fragmentos o partículas", y "constituyentes de interés". Un constituyente de interés se refiere al objetivo del muestreo, por ejemplo, determinar el contenido de oro, el contenido de cobre, el contenido de humedad, el tamaño de partículas, etc. En cambio, cuando hablamos de fragmentos o partículas, aunque realizáramos una selección equiprobable de los fragmentos a partir del lote, el constituyente podría no estar liberado y por lo tanto, después de realizada la selección, el constituyente podría no ser bien representado en la muestra.

b) analizar los errores asociados en cada operación selectiva (OS) y operación no selectiva (ONS)

Si analizamos las operaciones selectivas, vamos a encontrar, que en este tipo de operación sólo se pueden producir los siguientes errores:

1. El error fundamental

2. El error de segregación y agrupamiento

3. El error de delimitación de los incrementos

4. El error de extracción de los incrementos

5. El error de ponderación

Si analizamos las operaciones no selectivas, el único error que se puede asociar es:

6. El error de preparación de los incrementos.

En el caso de las OS, se debe analizar cada error por cada operación y ver cómo poder evitarlo para que el dispositivo o la técnica asociado a este tipo de operación no provoque desviaciones al proceso.

En el caso de las ONS, la estrategia sería dividir el proceso en etapas y en cada etapa ver qué tipo de alteración se produce o puede producir y realizar un análisis de criticidad de riesgos. Una clasificación práctica sería considerar alteraciones en la composición física (ACF), alteración en la composición química (ACQ), alteración en la data (ADD) u otros tipos de alteración según sea el alcance del muestreo.

Hay que entender que los dos primeros errores existen en la naturaleza, independiente del proceso de muestreo, por lo que estos errores no pueden ser eliminados. 

Los errores 3, 4, 5 y 6, por lo menos en teoría si pueden ser cancelados, si se respetan las reglas del muestreo correcto o los 2 principios del muestreo correcto, ya que estos errores son introducidos en el proceso de muestreo.

Conclusión.  Si cumplimos con los 2 principios del muestreo correcto o las 4 reglas de la corrección del muestreo de P. Gy, entonces, los únicos errores que prevalecerán serán el fundamental y el error de segregación y agrupamiento.

A gran escala

Clasificación de los lotes

Según la teoría de Pierre Gy, los lotes pueden ser vistos de tres formas diferentes, cada lote puede verse de forma continua o discontinua, ordenado o desordenado o verse según el número de dimensiones consideradas para su muestreo. 

Generalmente, es más fácil ver estos lotes desde el punto de vista continuo cuando analizamos estos fenómenos a gran escala (es decir, viendo los resultados de la planta como series, por ejemplo)

Ahora bien, según esta teoría, antes de aplicar estos principios o reglas de la corrección del muestreo, cuando se trata de lotes continuos, los lotes a ser muestreados deben ser transformados, en lo posible, primero a lotes de 1 dimensión o de 0 dimensión según corresponda.

Para entender esta clasificación de los lotes, partimos de la base de la existencia en nuestro universo de 3 dimensiones espaciales. Es decir, ancho, largo y profundidad (en la física corresponde a la presentación de los ejes x, y, z en un gráfico tridimensional).

Lote 3d

Un lote de 3 dimensiones (3d), es aquel donde en las 3 dimensiones no se cumple la regla 1 de la corrección del muestreo, es decir "todos los fragmentos o grupos de fragmentos no tienen la misma oportunidad de ser seleccionados y formar parte de la muestra" en los 3 ejes de coordenadas de un gráfico tridimensional.

Un ejemplo típico, es cuando se muestrea con una pala sobre una pila de acopio, una sonda que no alcanza a llegar el fondo en un maxisaco o en el cargamento de un camión, vagón de tren, motonave, etc. El uso de lanzas o medialunas para muestrear pulpas en la planta.

Lote 2d

Sin embargo, este lote 3d lo podemos transformar a un lote de 2 dimensiones si aplanamos el lote o alargamos el dispositivo de muestreo, de tal forma que ahora sí pueda llegar al fondo. En este caso, se cumple la regla 1, sólo en una de sus dimensiones. Es decir "todos los fragmentos o grupos de fragmentos no tienen la misma oportunidad de ser seleccionados y formar parte de la muestra" sólo en 2 de los ejes de coordenadas de un gráfico tridimensional.

Un ejemplo típico, es cuando la sonda para muestrear el maxisaco, la lanza o el cortador sobre un cargamento en un camión, vagón de tren, pila de acopio donde el dispositivo ahora sí llega al fondo.

Lote 1d

Pero, también podemos transformar un lote 3d o 2d en un lote de una dimensión si el lote lo alargamos y muestreamos ancho y espesor como se muestra en la figura. Es decir, en dos de sus dimensiones se cumpliría la regla 1. Y sólo en 1 dimensión los fragmentos o grupos de fragmentos no tendrían la misma oportunidad de ser seleccionados y formar parte de la muestra". O sea, en 1 de los ejes de coordenadas de un gráfico tridimensional.

Un ejemplo típico, el muestreo sobre una correa transportadora detenida, o en la descarga de una cinta transportadora donde se corta el ancho y espesor del material. Lo mismo puede aplicarse a las pulpas y líquidos donde el cortador debe interceptar el flujo en la descarga de ésta, cortando el ancho y el espesor.

Lote 0d

Un lote de 0 dimensión se refiere a aquel lote donde el número de dimensiones llega a ser irrelevante.

El orden de las unidades es irrelevante. Se pueden tratar como poblaciones estadísticas, donde cada unidad (no correlacionada) tiene la misma probabilidad de ser escogido.

Es de 0d en la medida que estos lotes sean considerados como unidades aleatorias y discontinuas.

Ejemplo de unidades que pueden ser enumeradas; maxisacos, camiones, tambores, vagones de tren. Pero cuando muestreamos al interior de estas unidades, pueden ser de 3d, 2d o 1d según la forma del lote o el dispositivo que usemos.

También podemos considerar lotes de 0d cuando los lotes son pequeños y pueden ser manipulados en su totalidad. Un ejemplo típico es homogenizar el lote para extraer una muestra representativa, siempre y cuando se encuentren en el lado seguro en un diagrama de muestreo respecto de la masa a tomar.

Conclusión. Si podemos transformar, en lo posible, los lotes a lotes de 1d, en la planta por ejemplo, entonces estamos en condiciones de identificar los siguientes errores:

7. El error de tendencia

8. El error de fluctuación periódica

Una forma de cuantificar estos errores es a través de un estudio variográfico. Este estudio además puede cuantificar los errores a pequeña escala. 

Para cuantificar el error de tendencia, hay que tomar tantos incrementos como sea posible. La variografía nos entrega una herramienta para determinar el intervalo de muestreo óptimo.

Para disminuir el error de fluctuación cíclica se debe realizar una investigación de sus causas para ver por qué se producen y así poder minimizarla.

Resumen de los errores de la teoría de Pierre Gy

En resumen, los errores son los que se presentan a continuación:

A pequeña escala:

1. Error fundamental, EF.- Error asociado a las diferencias entre fragmentos en cuanto a su forma, tamaño, densidad, composición química, propiedades físicas.

Es un error que se puede estimar con anterioridad, depende de cada unidad geológica.

2. Error de segregación y agrupamiento, ESG.- Error asociado a las diferencias entre grupos de fragmentos. Es un fenómeno cambiante y transitorio.

3. Error de delimitación de los incrementos, ED.- Es un error que se asocia a los dispositivos y técnicas. Se refiere a la forma no equiprobable de considerar la selección de los incrementos.

4. Error de extracción de los incrementos, EE.- Se asocia a los dispositivos de muestreo Se refiere a la forma incorrecta de extraer los incrementos al no respetar el principio de equiprobabilidad. 

5. Error de ponderación, EW.- Error que se produce cuando la masa o volumen del incremento no es proporcional al tonelaje o volumen que está siendo muestreado

6. Error de preparación de los incrementos, EP.- Error no asociado a las etapas de selección y que se relaciona con la alteración de las muestras debido a pérdida de finos, material, descomposición, oxidación, degradación, contaminación, manipulación, etc.

7. Efecto nugget in situ, EN.- Error asociado al muestreo que no toma en cuenta la presencia de pepitas (nuggets) aisladas (material no quebrado), o agrupaciones de vetillas o agrupación de partículas aisladas que no se encuentran diseminados por todo el material. 

A gran escala:

8. Error de fluctuación de la heterogeneidad de largo plazo, HFE2.- Error no aleatorio, de tipo continuo, asociado a la planta y que representa las tendencias entre unidades. También podría ser definido como la segregación a largo plazo.

9. Error de fluctuación de la heterogeneidad periódica, HFE3.- Error no aleatorio, de tipo continuo, caracterizado por ciclos que pueden ser originados por un sinnúmero de causas, como cambio de material a horas establecidas, acciones sobre el proceso a intervalos regulares, etc. 

A continuación, se presenta un resumen de los errores de Pierre Gy, sus causas y como minimizarlos o cancelarlos según corresponda:

Referencias:

(1) P. Gy. "Sampling of Particulates Material. Theory and Practice". Ed. 1979. Ed. Elsevier Scientific Publishing Company.

(2) P. Gy. "Sampling of heterogeneous and dynamic material systems. Theories of heterogeneity, sampling and homogenizing". Ed 1992. Ed. Elsevier Scientific Publishing Company.

(3) Curso: Teoría y práctica del muestreo en minería" de Mauricio Arancibia G. Curso-taller muestreo en minería (arech.cl)

TRANSFORMACIÓN DE BOX-COX CON EXCEL

Una de las herramientas más comunes que se usa en estadística para transformar datos no normales a datos normales es la famosa transformación de Box-Cox, que consiste en usar el siguiente estadístico como punto de partida, cuando λ ≠ 0.  

Donde Zi es el puntaje de una distribución normal estándar, G es la media geométrica, Yi son los datos originales y λ es un coeficiente que sirve para determinar la mejor ecuación para la transformación de los datos originales a datos que se pueden ajustar mejor a una distribución normal.

Cuando λ = 0 o muy próximo a 0, entonces, la transformación se puede calcular directamente por:

Para resolver esta ecuación de tipo iterativa y obtener un lambda óptimo, se procede de la siguiente manera.

Se fija un objetivo a minimizar que en este caso es la desviación estándar, la cual se obtiene para datos individuales a partir del rango móvil promedio y en el caso de subgrupos a partir del rango promedio, según la siguiente expresión:

Por lo tanto, la función objetivo, que es la desviación estándar estimada se minimiza cambiando el valor inicial de lambda.

Una vez terminada la iteración y obtenido el valor de lambda, éste se compara con los lambda de la siguiente tabla y se usa la expresión correspondiente más próxima. Por ejemplo, si el lambda obtenido es 1,7, se puede usar la expresión que corresponde a lambda = 2 para transformar los datos.

Aquí, Wi significa datos transformados.

Ejemplo en Excel

Antes de proceder a realizar estos cálculos en Excel, previamente se debe descargar el paquete estadístico SOLVER desde complementos de Excel. 

Archivo < Opciones < Complementos. En administrar hacer clic en IR, y luego clickear Solver y aceptar. El paquete estadístico quedará disponible en datos.

Para entender cómo se usa esta herramienta con Excel, supongamos que tenemos los siguientes datos, los cuales claramente no se ajustan a una distribución normal como se aprecia en el siguiente gráfico.

Si se realiza un test de normalidad a los datos, el p-valor Anderson Darling < 0,005

Para realizar la transformación, se deben colocar los siguientes datos en una planilla de Excel. En la columna A colocar los datos originales, y en la columna B calcular los Zi de acuerdo con la ecuación correspondiente, pero partiendo de la base de un valor inicial de iteración, que en nuestro ejemplo podría ser l = 0,5. Para calcular la desviación estándar (sigma) se debe proceder a calcular los rangos móviles de cada valor respecto del anterior en la columna C, luego calcular el rango móvil promedio, y ese valor dividirlo por d2 = 1,128 para obtener sigma. Ver la siguiente figura.

Una vez realizado todos estos cálculos se procede a usar la función SOLVER de Excel

Datos < Solver

Aquí de lo que se trata es minimizar el valor de sigma cambiando el valor de lambda, sujeto a la restricción de que lambda no puede ser mayor que 1. 

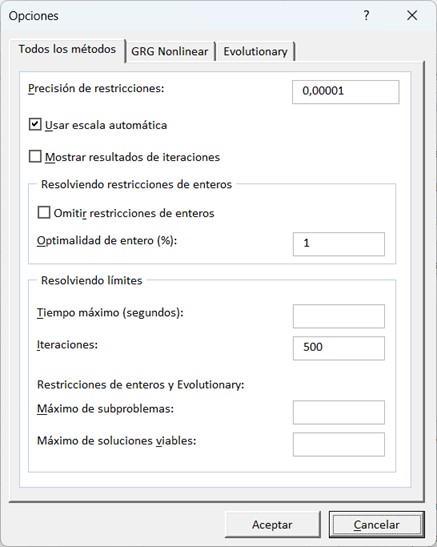
Las siguientes figuras muestran como completar los cuadros de diálogo para obtener el lambda que buscamos.

Colocando las siguientes restricciones

Aceptar, y en opciones colocar 500 iteraciones.

aceptar

Y finalmente, aceptar.

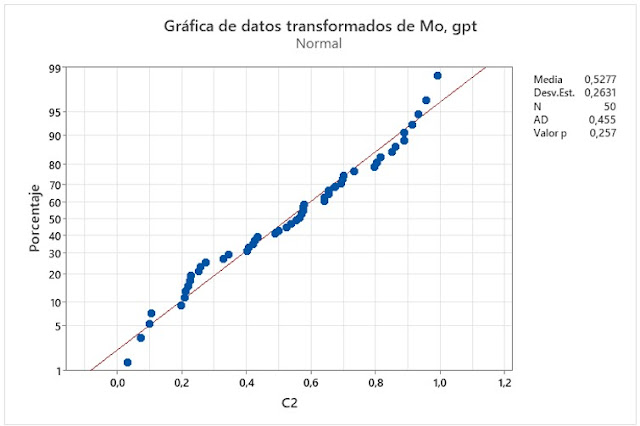
El resultado de lambda final para este ejemplo es 0,44. Como l = 0,44 está más próximo a l = 0,5. Por lo tanto, la transformación que procede es

Y los datos transformados serán

Los cuales según se puede ver en esta gráfica se ajustan mejor a una distribución normal que los datos originales.

Referencias:

(1) Solver - Soporte técnico de Microsoft

(2) Box-Cox Transformation | Real Statistics Using Excel (real-statistics.com)

(3) Curso "Estadística con Excel aplicado a procesos mneros" de Mauricio Arancibia G.

ENSAYO SOBRE UNA NUEVA PROPUESTA DE MEDICIÓN DE LA VARIABILIDAD E INCERTIDUMBRE

Ronald Fisher fue quien se dio cuenta que había que diferenciar entre población y muestra. Fue él, precisamente, quien introdujo los términos de parámetros (asociados a la población) y estadísticos (asociados a la muestra). A la vez, también se percató que los parámetros desconocidos, teníamos que "estimarlos" a partir de una muestra, proceso denominado "inferencia estadística".

Hasta aquí, tenemos una población con parámetros desconocidos, donde la estimación de los parámetros se hace a través de una muestra, cuyos términos a evaluar se denominan ahora "estadísticos". Y la inferencia estadística se denomina al proceso mediante el cual se hace afirmaciones válidas acerca de la población o proceso con base en la información contenida en una muestra.

Sin embargo, algo que no nos dicen los libros de estadística clásico o introductorio, la mayoría al menos, es que para poder estimar el valor del parámetro a partir de una muestra, debemos necesariamente realizar "MEDICIONES" sobre esta última. Y la inclusión de este nuevo factor en la estimación del parámetro, lo cambia todo, porque necesariamente se tiene que incorporar nuevas fuentes de ruido que hacen que la estimación se haga menos precisa.

De eso se trata este artículo, de identificar cuáles son esas fuentes de variaciones e incertidumbres que se nos presentan en la minería y la industria para que podamos medirlas de la forma más óptima posible. 

ESTIMACIÓN DE LOS PARÁMETROS DE UNA POBLACIÓN EN AUSENCIA DE SESGO

En este primer apartado, vamos a tratar de la estimación de los parámetros, media y variación natural de la característica de interés, de una población, estática o dinámica (proceso). Y esta estimación la vamos a realizar en ausencia de sesgo para facilitar nuestro análisis del modelo.

Por lo tanto, la secuencia para realizar una estimación del parámetro en el mundo real es: 

POBLACIÓN - Muestreo - MUESTRA - Medición - RESULTADO

La siguiente figura corresponde a un modelo, todavía en calidad de borrador, que muestra tentativamente los factores involucrados en la estimación de parámetros de una población a través de una muestra. Lo que interesa aquí es estimar tanto la media como la variación de la característica en esa población.

Ojo con esta clasificación. La incertidumbre sólo se aplica a la segunda fila, es decir, sólo a la estimación de la variación natural de la característica de interés en el muestreo y en el sistema de medición. En cambio, el error estándar de la media no debería formar parte de ésta, porque se debería entender, en base a este modelo, que la incertidumbre corresponde a la semi - proporción o a la mitad del intervalo de tolerancia estadístico, que debería ser expresado con un intervalo de confianza dado, Intervalo que debería ser mucho más pequeño, insignificante, comparado con el intervalo de tolerancia dado para que la estimación tenga sentido práctico. Cuando el intervalo de confianza no cumple con esta condición, entonces, y sólo entonces, este intervalo debería sumarse al del intervalo de tolerancia estadístico.

Figura 1 - Estimación de la media de la característica de interés y la variación natural de la característica de interés en la población. La primera fila trata de la estimación de la media de la población, mediante x̄ . La segunda fila trata en cambio de la variación de los valores individuales, X

donde: 

      µ                 : Media de la población

      x̄                 : Media de la muestra

      σ_NAT (P)     : Variación natural de la población

      S_NAT (P)    : Variación natural de la muestra que representa a la de la población

      S_NAT (M)   : Variación natural asociada al muestreo (incertidumbre del muestreo)

      S_NAT (SM) : Variación natural del sistema de medición (incertidumbre del sistema de medición)

      S_NAT (T)     : Variación natural total

      S_x̄                : Variación debido a la estimación de la media (Error estándar de la media)

En esta figura, se presenta la estimación de la variación natural de la característica de la población considerando todas las etapas hasta obtener un resultado. Como se puede apreciar, en el proceso de muestreo se introduce una variación adicional que corresponde a la variación natural del muestreo. Sin embargo, en el proceso de medición se vuelve a introducir una nueva variación, que corresponde a la variación natural del sistema de medición. 

En todas estas etapas se han introducido variaciones que he denominado "natural" para diferenciarla de un cuarto componente, que no corresponde a la variación natural de las etapas anteriores, que es la que se asocia a la estimación del parámetro a través de un estadístico, en este caso, la desviación estándar de la media (error estándar de la media).

Diferenciar entre variación natural y variación para la estimación del parámetro es importante por varias razones. 

1. Las variaciones naturales son constantes a estimar, no dependen del tamaño de muestra. En cambio, la variación debido a la estimación del parámetro (error estándar de la media) depende fuertemente del tamaño de muestra.
2. La variación para la estimación de la media poblacional sólo nos dice que tan confiables es el resultado obtenido. En cambio, la variación natural está asociada con la variabilidad de los procesos.

Veamos de qué depende cada variabilidad.

Variación asociada a la estimación de la media depende:

        a) de la variación natural total o de la variación natural de cada proceso, según corresponda

        b) del tamaño de muestra, n

        c) del Nivel de confianza, 1 - α

Variación natural (de la característica de interés) asociada al sistema de medición depende:  

        a) de la variación (de la característica de interés) asociada a equipos

        b) de la variación (de la característica de interés) asociada a operadores

        c) de la variación (de la característica de interés) asociada a método

        d) de la variación (de la característica de interés) asociada a factores ambientales

        e) de otras fuentes

Variación natural (de la característica de interés) asociada al muestreo depende:    

        a) de la variación (de la característica de interés) asociada a las operaciones selectivas

            (debido al error fundamental, de segregación/agrupamiento, de delimitación, de extracción,

            de ponderación,)

        b) de la variación (de la característica de interés) asociada a las operaciones no selectivas 

            (debido al error de preparación)

        c)  de la variación (de la característica de interés) asociado a modelos continuos a gran escala

             (de tendencia y/o cíclico)

En resumen, la variación total, en ausencia de sesgo, asociada a un resultado va a depender de 3 variaciones.

1. De la variación natural de los valores originales (de la característica de interés) de la población o proceso 
2. De la variación natural (de la característica de interés) en el muestreo (incertidumbre del muestreo)
3. De la variación natural (de la característica de interés) en el sistema de medición (incertidumbre del sistema de medición)

Sin embargo, minimizar las diferentes fuentes de variación e incertidumbre va a depender del objetivo que se persiga. A saber:

1. Si queremos que nuestra estimación de la media y de la variación natural de la característica de interés en nuestra población o proceso originales sea lo más precisa posible, entonces debemos minimizar las variaciones 2 y 3.
2. Si solo estamos interesados en estimar la variación o incertidumbre de la característica de interés introducida por el muestreo, entonces 1 y 3 deberán ser insignificantes,
3. Y cuando nuestro objetivo, o nuestra población sea estimar la variación o incertidumbre de la característica de interés del sistema de medición, entonces, 1 y 2 deberán ser insignificantes.
4. Sin embargo, si nuestro interés es estimar la variación de la característica de interés del muestreo más la del sistema de medición, entonces sólo 1 deberá ser insignificante o cero.

En todos estos casos, lo que estamos calculando es la variación natural de la característica de interés, asociadas al intervalo de tolerancia estadístico, y que corresponde a la proporción p de estas poblaciones (1, 2 o 3 o sus combinaciones). Pero, cada una de las estimaciones de esas proporciones deberá estar acompañada por una estimación por intervalos (o intervalo de confianza) de la media, debiendo ser esta última insignificante para que el resultado tenga sentido práctico.

Cuando la estimación por intervalos de la media (o intervalo de confianza) no es insignificante, sólo entonces debería sumarse a las variaciones e incertidumbres anteriores.

Conclusión

Por lo tanto, la variación total de la característica de interés respecto a la media, en ausencia de sesgo, va a depender del objetivo que se persiga. Sin embargo, en todos estos casos debemos diferenciar entre intervalo de confianza e intervalo de tolerancia estadístico. En todos estos casos, lo que nos interesa es calcular la proporción p de la población escogida (1 a 4) pero con un nivel de confianza dado (ya que se trata de una muestra).

Es importante destacar que el intervalo de confianza sea lo más pequeño posible, o por lo menos mucho menor que el intervalo de tolerancia estadístico obtenido, insignificante, para que este resultado tenga sentido práctico. Si ese no fuera el caso, sólo entonces, debería sumarse el intervalo de confianza a la variabilidad total.

Para una mejor comprensión de este artículo, favor leer: 

NO CONFUNDAS INTERVALOS DE CONFIANZA CON INTERVALOS DE TOLERANCIA ESTADÍSTICO

Referencias

1. Meeker, Hans, Escobar - Statistical Intervals_ A Guide for Practitioners and Researchers - Ed. 2017
2. Montgomery, Runger - Applied Statistics and Probability for Engineers, - 7ª Ed, 2018
3. Walpole, Myers, Myers, Ye - Probability & Statistics for Engineers & Scientists - Ed. 2016
4. Norma ISO 16269-6:2014 - Statistical interpretation of data — Part 6: Determination of statistical tolerance intervals - Ed 2014

ESTADÍSTICA DE DUPLICADOS PARA EL CONTROL DE CALIDAD DE MUESTRAS GEOQUÍMICAS

El presente artículo tiene por objeto mostrar la estadística que actualmente se usa en el tratamiento de los datos en muestras geoquímicas para determinar la precisión en condiciones de repetibilidad o reproducibilidad en base sólo a muestras duplicadas.

Algunos de los estadísticos más comunes que aparecen en este control, son, la media aritmética, la desviación estándar, el rango, el error relativo, el coeficiente de variación y la varianza relativa.

La siguiente tabla presenta un resumen de estos estadísticos en base sólo a pares de duplicados:

Nota (1). - X₁ es el dato original y X₂ es el dato duplicado.

Desde el punto de vista práctico, principalmente existen tres tipos de errores que deben ser considerados ya sea en la implementación y/o mantención de cualquier sistema de control de calidad; el error sistemático, el error aleatorio y el error grueso.

El error sistemático, es aquel error en donde los valores de las observaciones tienden a ser persistentemente más altos que la media esperada o persistentemente menor que esta. Las causas pueden ser variadas, como un equipo descalibrado, un material de referencia no válido, un método analítico no adecuado, temperaturas no controladas, etc. Este error puede ser corregido. 

El error aleatorio, en cambio, es aquel error donde los resultados individuales caen a ambos lados de la media, regidos sólo por el azar, de acuerdo con un tipo de distribución. Este error puede ser mejorado, pero nunca cancelado, ya que está asociado a las limitantes propias de cada proceso.

Por último, el "error grueso" o "error grosero" es aquel que está asociado a los errores personales, a las equivocaciones, tales como una mala transcripción de los datos, un intercambio de muestras, errores de tipeo, etc. Es decir, errores que son ajenos a la población o al proceso mismo. Estos errores se deben identificar, investigar sus causas y evitar su recurrencia a través de un sistema de calidad preventiva. Este error puede ser minimizado si se cuenta con un buen sistema de calidad.

Por lo tanto, con estos antecedentes, el objetivo de cualquier sistema de control de calidad es la de identificar estos tipos de errores y corregirlos y/o minimizarlos según corresponda.

A continuación, se presentan algunas herramientas de control que pueden ser útiles en la detección y corrección principalmente de este tipo de errores, pero que están asociados principalmente a la estadística de los pares de duplicados.

a) Análisis de la dispersión de duplicados

Los pares de datos, original y duplicado pueden ser analizados mediante un gráfico de dispersión, donde en el eje de la ordenada se coloca el valor duplicado y en el eje de la absisa, el valor original. 

Estos valores se plotean en este tipo de gráfico, y se traza una línea 1:1, de 45 grados respecto a la horizontal con el fin de visualizar si existen ciertos patrones que puedan caracterizar el conjunto de los datos, como, por ejemplo, verificar el tipo y magnitud de la dispersión respecto a lo esperado, presencia de error sistemático y/o presencia datos anómalos (outliers).

En el caso de usar un análisis de regresión a los datos pareados, para visualizar la existencia de sesgo estadístico, se debe partir de la base que, en el concepto de regresión, ambos pares no pueden ser tratados de la misma forma, ya que una de las variables debe definirse como aleatoria (variable respuesta) en función de la otra variable que es definida como fija (variable predictora). En nuestro caso, es el valor duplicado, la que se debe escoger como una variable aleatoria o variable respuesta y el valor original como fijo, y no viceversa.

Una desventaja de este gráfico, si se usan los límites de control tal cual se muestra en la figura, es que los valores de aquellas muestras con concentraciones cerca del límite de detección van a tender a ser rechazadas en circunstancias que pueden ser muestras completamente válidas. Para evitar esto último, se recomienda usar líneas de control de función hiperbólicas (Ver método hiperbólico).

b) Gráfico MIN-MAX

Este gráfico considera en el eje de la absisa colocar el valor mínimo y en el eje de las ordenadas el valor máximo correspondientes a un par de duplicados.

1. En Excel, disponer de los pares de resultados, por ejemplo, en una columna A el original y en una columna B el duplicado.
2. En una columna C, calcular el máximo por cada par de resultados
3. En otra columna D, calcular el mínimo por cada par de resultados
4. Plotear en un gráfico los valores máximos versus el mínimo
5. Considerar una recta 1:1 de 45°

c) Gráfico hiperbólico

Este método considera que, a bajas concentraciones, es altamente probable que muchas observaciones de muestras completamente válidas con el gráfico anterior pueden quedar fuera de los límites de control, debido a que a bajas concentraciones la dispersión de los resultados tiende a aumentar. Para evitar este problema, se construye este gráfico en la que el límite de control obedece a una función hiperbólica de la forma y² = x²m² + b², donde m es la pendiente, x es el valor mínimo de la observación y b el intercepto.

d) Análisis de la Diferencia relativa absoluta (ARD) versus el porcentaje de datos acumulados

Para construir esta relación en un gráfico, se debe estimar la diferencia relativa absoluta de los pares de duplicados y graficarlo en función del porcentaje acumulado como sigue:

1. Calcular el error relativo (diferencia relativa absoluta) para cada par de duplicados y colocarlo en una columna de Excel
2. Ordenar el error relativo de menor a mayor
3. En otra columna calcular el porcentaje de datos acumulados según la posición que tiene el error relativo.
4. Plotear en un gráfico el error relativo, en porcentaje versus el % de datos acumulados
5. Evaluar el desempeño de los datos duplicados en base al criterio previamente establecido para los diferentes tipos de duplicados.

Reglas recomendadas: 

Dup pulpas : >90 % de los datos con un ER<10%

Dup preparación -8#Ty: >90 % de los datos con un ER<20%

Dup terreno/Muestras gemelas: >90% de los datos con un ER<30%

e) Gráfico de la diferencia relativa versus la ley promedio

Otro de los gráficos que pueden ser útiles para ver el comportamiento de los datos es el de la diferencia relativa versus la ley promedio del elemento de interés. 

Regla

Lo que se espera es que, a bajas concentraciones la dispersión tiende a aumentar. Un patrón diferente estaría indicando que existe una causa asignable que debería ser investigada.

f) Análisis de la precisión de Howarth-Thompson

Este método, al igual que los gráficos de dispersión anteriores tiene por objeto establecer límites de control para rechazar aquellas observaciones (y muestras) que son inconsistentes con lo que se espera en el proceso. Estas muestras deberían ser nuevamente chequeadas en el laboratorio.

Para la construcción de este gráfico de control, la curva se obtiene a partir de datos históricos, donde el CV (Precisión de HT) se plotea en función de la concentración media.

El Control de calidad se puede efectuar en base al estadístico muestral ARD o HARD, que es representado por cada punto en el gráfico. Si El ARD o HARD, según corresponda es mayor al límite de la curva, entonces esa muestra se rechaza.

Nota. - Para más información sobre este estadístico, ver mi otro post: 

Estimación de la precisión mediante el estadístico de Howarth-Thompson

Cuantificación de la precisión

Para estimar la precisión de las diferentes etapas del proceso se deben tener en consideración las siguientes observaciones:

1. La precisión del proceso sólo tiene sentido si el proceso es estable y si está libre de observaciones anómalas que no pertenecen al proceso mismo. En otras palabras, está asociada al error aleatorio. Por lo tanto, es importante que para estimar la precisión deben eliminarse aquellos outliers, que no forman parte del proceso.
2. La precisión es función de la concentración. A medida que la concentración disminuye, el CV tiende a ser más grande. Por lo tanto, se recomienda para cuantificar y comparar la precisión a través del tiempo, hacerlo no sólo de una manera global, sino por rangos de concentración adecuados.
3. Si se quiere estimar la precisión de los duplicados de preparación, deberá entenderse que la precisión así obtenida en el laboratorio corresponde a la suma de la precisión de la preparación y del análisis. Por lo que para obtener la precisión sólo de la preparación de muestras, la precisión total deberá restarse a la precisión del análisis.
4. Si se quiere estimar la precisión de los duplicados de terreno, deberá entenderse que la precisión así obtenida en el laboratorio corresponde a la suma de la precisión del muestreo, de la preparación y del análisis. Por lo que para obtener la precisión sólo del muestreo, la precisión total deberá restarse a la precisión de la preparación y del análisis.
5. Hay dos formas de restar estas precisiones a la precisión total para obtener las precisiones de preparación y de terreno, a) haciéndolo de una manera aproximada, considerando una estimación media del análisis y preparación en el mes por ejemplo y b) considerando un modelo anidado de acuerdo con la siguiente figura. Aquí la forma de generar los duplicados de preparación es hacerlo sobre los duplicados de terreno ya existentes, y para generar los duplicados de análisis hacerlo sobre los duplicados a la vez de preparación ya existente

Para obtener una estimación de la precisión, la recomendación es hacerlo por niveles de concentración, ya que la precisión que engloba todas concentraciones del elemento de interés puede ir cambiando a través del tiempo, ya que las leyes pueden ir disminuyendo a medida que la mina va envejeciendo.

Una forma de medir esta precisión es calcular la varianza relativa por cada par de duplicados y al final estimar la precisión como coeficiente de variación promedio.

Referencias

1. Abzalov M – Applied Mining Geology-Springer International Publishing – Ed. 2016.
2. MRDI - Assay Quality Assurance Quality Control Program for drilling projects at the pre-feasibility report level – 3°Ed.2000
3. Thompson M, Howarth R. -Duplicate Analysis in Geochemical Practice. Part 1. Theoretical Approach and Estimation of Analytical Reproducibility. Ed 1976.
4. ISO 12744:2006 - Copper, lead, zinc and nickel concentrates — Experimental methods for checking the precision of sampling
5. Curso-Taller de Tratamiento de datos con Excel para Control de calidad aplicado a procesos mineros de Mauricio Arancibia G.

CARTAS DE CONTROL DE SHEWART PARA VALORES INDIVIDUALES EN EXCEL

La idea tradicional de inspeccionar el producto final y eliminar las unidades que no cumplen con las especificaciones una vez terminado el proceso, se reemplaza por una estrategia más económica de prevención antes y durante del proceso industrial con el fin de lograr que precisamente estos productos lleguen al consumidor sin defectos.

Así las variaciones de calidad producidas antes y durante el proceso pueden ser detectadas y corregidas gracias al empleo masivo de Gráficas de Control.

Según este nuevo enfoque, existen dos tipos de variabilidad. El primer tipo es una variabilidad aleatoria debido a "causas al azar" o también conocida como "causas comunes". El segundo tipo de variabilidad, en cambio, representa un cambio real en el proceso atribuible a "causas especiales", las cuales, por lo menos teóricamente, pueden ser identificadas y eliminadas.

Los gráficos de control ayudan en la detección de modelos no naturales de variación en los dato que resultan de procesos repetitivos y dan criterios para detectar una falta de control estadístico. Un proceso se encuentra bajo control estadístico cuando la variabilidad se debe sólo a "causas comunes".

Los gráficos de control de Shewart son básicamente de dos tipos; gráficos de control por variables y gráficos de control por atributos. Para cada uno de los gráficos de control, existen dos situaciones diferentes; a) cuando no existen valores especificados y b) cuando existen valores especificados.

Se denominan "por variables" cuando las medidas pueden adoptar un intervalo continuo de valores; por ejemplo, la longitud, el peso, la concentración, etc. Se denomina "por atributos" cuando las medidas adoptadas no son continuas; ejemplo, tres tornillos defectuosos cada cien, 3 paradas en un mes en la fábrica, seis personas cada 300, etc.

Antes de utilizar las cartas de control de valores individuales por variables, debe tenerse en consideración lo siguiente:

1. Los datos deben ser continuos
2. Los datos deben estar en orden cronológico
3. Los datos se deben recolectar en intervalos de tiempo igualmente espaciados
4. Los datos deben ser observaciones individuales que no se recolectan en subgrupo
5. Los datos deben incluir al menos 100 observaciones totales
6. Los datos deben ajustarse a una distribución normal o aproximadamente normal
7. Las observaciones no deben estar correlacionadas entre sí 

Las etapas que deben tomarse en cuenta para mejorar el proceso están esquematizadas en la siguiente figura:

Para construir una carta de control, se parte de la base que el proceso debe ajustarse a algún tipo de distribución y que el comportamiento de los datos a través del tiempo debe ser aleatorio. Si la distribución de los datos se puede ajustar a una normal, entonces los límites de control será la consignada en la siguiente expresión:

donde LC son los Límites de control, μ es la media poblacional, sigma la desviación estándar poblacional y 3 corresponde al número de desviaciones estándar, cuyo intervalo +/- 3 respecto de la media concentra el 99,73% de los datos.

Nota.- En estadística se sabe que s no es un buen estimador de sigma, porque es insesgado, y además para estimar sigma a partir del rango móvil promedio, para esta estimación, el rango móvil promedio cada dos observaciones consecutivas se dividide por un factor d2 que es igual a 1,128.

Cartas de control de valores individuales por variables sin especificación en Excel

Si las cartas no usan especificaciones, entonces se puede usar la media aritmética y la desviación estándar del mismo proceso.

A continuación, se presenta la forma como se pueden construir estas cartas en Excel

El siguiente ejemplo utiliza 50 datos de contenido de hierro, expresado en porcentaje, que corresponde a los valores obtenidos de un material de referencia ensayado en un laboratorio en particular:

Datos:

Cálculos en Excel:

Con estos datos, podemos construir las cartas de control respectivas.

Insertar > Gráficos > Dispersión. Luego seleccionar datos:

Para los datos, agregar serie, en el eje x colocar A2:A51. En el eje y colocar B2:B51. Aceptar

Para la media, agregar serie, en el eje x colocar H5:H6. En el eje y colocar I5:I6. Aceptar

Para el LIC, agregar serie, en el eje x colocar H5:H6. En el eje y colocar J5:J6. Aceptar

Para el LSC, agregar serie, en el eje x colocar H5:H6. En el eje y colocar K5:K6. Aceptar

Aceptar.

Hacer clic sobre el punto de la media en el gráfico, botón derecho del mouse, dar formato a serie de datos, tacho de pinturas, líneas, línea sólida, rojo. Luego sin salir de la línea, ir a marcador, opciones del marcador, colocar ninguno.

Hacer clic sobre el punto del LIC, botón derecho del mouse, dar formato a serie de datos, tacho de pinturas, líneas, línea sólida, azul. Luego sin salir de la línea, ir a marcador, opciones del marcador, colocar ninguno.

Hacer clic sobre el punto del LSC, botón derecho del mouse, dar formato a serie de datos, tacho de pinturas, líneas, línea sólida, azul. Luego sin salir de la línea, ir a marcador, opciones del marcador, colocar ninguno.

Hacer clic sobre los puntos de los datos, ir a líneas, línea sólida, en ancho colocar 0,75 pt. Ir a marcador, en borde colocar ninguno y en relleno colocar el color a elección.

Hacer clic sobre el eje x, dar formato eje, en mínimo colocar 1 y en máximo colocar 51.

Carta de rango móvil

Para la carta de Rango móvil, se parte de la base que como son valores individuales, el rango se calcula a partir de la diferencia absoluta de dos observaciones consecutivas. 

El límite superior se calcula según la siguiente expresión:

LSC = D4 x RM prom

donde D4 es un factor igual a 3,267.

Para construir la carta de control rango móvil:

Insertar > Gráficos > Dispersión. Luego seleccionar datos:

Para los datos, agregar serie, en el eje x colocar A2:A51. En el eje y colocar C2:C51. Aceptar

Para el LSC, agregar serie, en el eje x colocar H5:H6. En el eje y colocar M5:M6. Aceptar

Aceptar.

Hacer clic sobre el punto del LSC, botón derecho del mouse, dar formato a serie de datos, tacho de pinturas, líneas, línea sólida, rojo. Luego sin salir de la línea, ir a marcador, opciones del marcador, colocar ninguno.

Hacer clic sobre los puntos de los datos, ir a líneas, línea sólida, en ancho colocar 0,75 pt. Ir a marcador, en borde colocar ninguno y en relleno colocar el color a elección. Aceptar 

Hacer clic sobre el eje x, dar formato eje, en mínimo colocar 1 y en máximo colocar 51.

Test de Nelson para detectar causas especiales

La siguiente tabla muestra aquellas condiciones que dan cuenta cuando un proceso se encuentra fuera de control estadístico, en la cual se debe tomar una acción correctiva o preventiva según corresponda.

Referencias

1. ISO 7870-2:2023 Control charts - Part 2: Shewhart control charts
2. Alwan L. - Statistical Process Analysis - Ed. 2000
3. Minitab 21 referencia
4. Curso de Control de calidad con Excel de Mauricio Arancibia G. - Ed. 2023

 

NO CONFUNDAS INTERVALOS DE CONFIANZA CON INTERVALOS DE TOLERANCIA ESTADÍSTICO

Uno de los grandes errores que se comete en el mundo de la ingeniería y de las ciencias es confundir estos dos tipos de intervalos.

La mayoría de los usuarios de métodos estadísticos están familiarizados con los intervalos de confianza (comunes) para la media de la población y para la desviación estándar de la población, pero a menudo no para los cuantiles de la población o la probabilidad de exceder un valor umbral especificado. A pesar de que algunas personas, especialmente en la industria, también conocen los intervalos de tolerancia, tienden frecuentemente a confundir estos intervalos, calculando un intervalo de confianza para contener la media poblacional cuando el problema requiere un intervalo de tolerancia o un intervalo de predicción.

Este artículo tiene por objeto, mostrar cuáles son esas diferencias y como se aplican en el mundo real.

Pero primero partamos definiendo qué entendemos por intervalo de confianza y qué entendemos por intervalo de tolerancia estadístico.

Un Intervalo de confianza, IC, es un intervalo donde podemos suponer de manera razonable que se encuentra el valor verdadero. Y cuando hablamos de un IC del 95% lo que estamos diciendo es que, si el experimento se repitiera varias veces, existe la probabilidad de que el 95% de esos intervalos pueda contener el valor verdadero.

En palabras simples, la longitud de ese intervalo es una medida de la precisión de la estimación del parámetro a través del estadístico.

En cambio, un intervalo de tolerancia estadístico (o simplemente intervalo de tolerancia para muchos textos), IT, es un intervalo que contiene una proporción específica de una población con un nivel de confianza establecido.

Para entender ambos conceptos, supongamos que tenemos un contenedor que contiene un cierto tipo de mineral, cuya característica de interés se encuentra uniformemente diseminado en el medio y que este lote lo podemos ver como una población probabilística (lotes de 0-D en la teoría de Pierre Gy), y estamos interesados en saber 2 cosas respecto de él:

Pregunta a) Cual es el contenido de arsénico medio en gpt; y

Pregunta b) Cuál es su variabilidad o dispersión en ese contenedor

Supongamos que los datos se pueden ajustar a una distribución aproximadamente normal, por lo tanto, para estimar los respectivos parámetros (valores que son desconocidos para nosotros) en a) podemos usar la media aritmética muestral para estimar la media poblacional μ, y para b) podemos usar la desviación estándar muestral para estimar la desviación estándar poblacional, σ.

Pero, también podemos hacer dos preguntas adicionales acerca de los datos del contenido de arsénico del contenedor:

Pregunta c) Qué tan confiable es el valor medio de arsénico reportado y

Pregunta d) Qué tan confiable es la desviación estándar de arsénico reportada.

Para las preguntas a y b estamos ante la presencia de estimaciones puntuales. Existe una estimación puntual para la media y una estimación puntual para la desviación estándar. Pero como la estimación puntual es un solo número, el hecho de repetir varias veces este experimento, vamos a obtener diferentes estimaciones puntuales y dependiendo del tamaño de muestra elegido esas diferencias podrían ser grandes o pequeñas. Por ello, la respuesta a las preguntas c y d están relacionadas con otro tipo de estimación; la estimación por intervalos (o intervalos de confianza) de la media y la estimación por intervalos (o intervalos de confianza) de la desviación estándar.

Sin embargo, todavía podemos hacer una quinta pregunta diferente a las anteriores:

Pregunta e) Cuáles son los valores extremos de contenido de arsénico que se presentan en el contenedor, que equivale a preguntar en qué intervalo se presenta el contenido de arsénico. Pero también podríamos preguntar por una proporción específica, no necesariamente sus extremos.

Partiendo de la base que se trata de un material heterogéneo, (y que la variabilidad del sistema de medición (conformada por operador, equipos y otros factores) es despreciable. La respuesta a e) corresponde a estimar el intervalo de tolerancia estadístico. Pero como igual debemos tomar una muestra, la respuesta más precisa obedece al área de las probabilidades. Es decir, igual debemos establecer un nivel de confianza dado para entregar esa proporción.

Matemáticamente equivale a estimar en forma simultánea μ y σ, que son desconocidos. Y eso se hace a través del factor k de la siguiente expresión:

donde k es un factor que se puede obtener de tablas estadísticas y depende de alfa y del tamaño de muestra.

 

Demostración de las diferencias entre IC e IT

Para realizar una demostración de las diferencias entre ambos intervalos, vamos a partir del principio que, si el tamaño de muestra tiende a infinito, la estimación de μ con la media muestral y de σ con s coinciden respectivamente.

Matemáticamente, si queremos calcular el intervalo de tolerancia estadístico del 95% para una muestra con media = 100 y desviación estándar = 5 para un número infinito de observaciones, no importa el nivel de confianza. El resultado es:

IT = 100-1,96*5, 100 + 1,96*5 = (90.2, 109.8)

En cambio, para el intervalo de confianza de la media y de la desviación estándar (no importa el nivel de confianza escogido) el resultado es cero.

IC para la media = (100.0, 100.0) que es equivalente a 100 +/- 0

IC de la desv. estándar = (5.0, 5.0)

El siguiente ejercicio se realizó usando el software Minitab. Se tomó una muestra lo suficientemente grande para que estas estimaciones de μ y σ sean lo más confiable posible. Se generaron 10.000.000 de números aleatorios para una distribución normal con media = 100 y desviación estándar = 5.

Con estos datos se realizó una estimación por intervalos con diferentes niveles de confianza; 0,90, 0,95 y 0,99.

Como se puede apreciar con tamaños de muestra muy grandes, los límites de confianza inferior y superior son muy semejantes. Es decir, el intervalo de confianza es demasiado pequeño.

Lo mismo se realizó para la estimación por intervalo de la desviación estándar.

donde se aprecia que los límites de confianza inferior y superior son semejantes, independientes del nivel de confianza,

Ahora bien, al calcular el intervalo de tolerancia estadístico para 10.000.000 de observaciones generadas aleatoriamente con diferentes niveles de confianza encontramos que los valores no dependen del nivel de confianza porque tienden a converger a un valor específico. 

Conclusión, el intervalo de tolerancia estadístico tiende a una proporción constante cuando n tiende a infinito, no importa el nivel de confianza.

En cambio, el intervalo de confianza tiende a ser cero.

Aplicaciones en el mundo real.

El siguiente ejemplo tiene por objetivo a ayudarnos a clarificar estas diferencias.

Tema. - Un material de referencia elaborado en un laboratorio para el elemento hierro.

Descripción. - Un material que es preparado en un laboratorio como material de referencia y que ese mismo material es ensayado diferentes veces por diferentes operadores, en diferentes días para obtener una media (valor asignado al MR) y una desviación estándar para ese laboratorio.

Datos; 

Objetivos:

Pregunta a) Cuál es el contenido medio de hierro en el Material de referencia. Esto equivale a determinar la media aritmética, que corresponde al valor central de los datos.

Respuesta: X barra = 12,51% Fe

Pregunta b) Cuál es su variabilidad o dispersión. Esto equivale a determinar la reproducibilidad media a través de la desviación estándar, que corresponde a la variación debida al sistema de medición, partiendo de la base que la no homogeneidad del MR es despreciable y que toda la variabilidad se deba al sistema de medición (operadores, equipos, método, otros factores).

Respuesta:  s =0,18% Fe

Pregunta c) Qué tan confiable es el valor medio de hierro reportado. Esto equivale a realizar una estimación por intervalos de la media, que es lo mismo que determinar el intervalo de confianza de la media. 

Respuesta: (12,47 a 12,54) % Fe con un 95% de confianza

Eso equivale al semi-intervalo +/- 0,03% Fe

Pregunta d) Qué tan confiable es la desviación estándar de hierro reportado. Esto equivale a realizar una estimación por intervalos de la desviación estándar, que es lo mismo que determinar el intervalo de confianza de la desviación estándar.

Respuesta: (0,16 a 0,21) % Fe con un 95% de confianza

Pregunta e) Cuáles son los valores extremos de contenido de hierro que se obtuvieron en la estandarización (asociado al sistema de medición).  Pero también podríamos preguntarnos por una proporción específica. Esto equivale a preguntar cuál es el intervalo de tolerancia estadístico.

Respuesta: Con un 95 % de confianza (1 - α = 0,95), se puede afirmar que el 95% de los valores (p = 0,95) producto del sistema de medición cubren un intervalo que va desde 12,11 a 12,91 % Fe. 

Con un 95% de confianza, se puede afirmar que el 99% de los valores se encuentran entre 11,98 a 13,04 % Fe.

Referencias

(1) Meeker, Hans, Escobar - Statistical Intervals_ A Guide for Practitioners and Researchers - Ed. 2017

(2) Montgomery, Runger - Applied Statistics and Probability for Engineers, - 7ª Ed, 2018

(3) Walpole, Myers, Myers, Ye - Probability & Statistics for Engineers & Scientists - Ed. 2016

(4) Norma ISO 16269-6:2014 - Statistical interpretation of data — Part 6: Determination of statistical tolerance intervals - Ed 2014

(5) Curso de Estadística con Excel aplicado a procesos mineros de Mauricio Arancibia G.

Pincha aquí para saber más acerca de los cursos que se ofrecen en 2023: CURSOS ONLINE