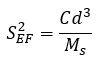El diagrama de muestreo preferido de Pierre Gy

Los diagramas de muestreo son herramientas bastante útiles que se usan principalmente en la industria minera con el propósito de presentar un protocolo válido de todo el proceso de muestreo en función de la masa de la muestra y del tamaño de partícula.

Un diagrama clásico que relaciona la varianza relativa del error fundamental con respecto a la masa de la muestra y al tamaño de partícula está consignada en la siguiente expresión:

   

Sin embargo, existe otro tipo de diagrama de muestreo que es equivalente al anterior y que se le conoce en la literatura como el "diagrama preferido de Pierre Gy", pero que relaciona la masa de la muestra con respecto al tamaño de partícula y a la varianza relativa del error fundamental, y cuya expresión está dada por:

Para construir este último diagrama de muestreo, y considerando una masa del lote que es al menos 10 veces la masa de la muestra, se partió de la base que la primera ecuación ya no nos servía para este propósito, debido a que la constante C depende del tamaño de partícula y lo que necesitamos es relacionar la masa de la muestra precisamente con diferentes tamaños.

Por lo tanto, para encontrar una expresión donde la varianza relativa del error fundamental no se encuentre relacionada directamente con la constante C, se procedió a la descomposición del término C, agrupando los términos que realmente son independientes del tamaño de partículas, tal como se ilustra en la siguiente expresión

Aquí los términos del numerador son independientes de d, por lo que se puede agrupar en una nueva constante K que es independiente del tamaño de partícula:

Por lo tanto, se obtiene una ecuación equivalente de la clásica pero en función de términos independientes de C.

simplificando, obtenemos:

Por lo tanto, la expresión final para este diagrama de Ms vs d queda establecido por la ecuación:

Si queremos construir, por ejemplo, un diagrama de muestreo para el cobre en un mineral de cobre que se encuentra uniformemente diseminado, entonces podríamos aproximar el exponente r = 0,5.y la expresión anterior quedaría como:

Y de acuerdo con esta expresión se construye el siguiente diagrama de muestreo, en la que la masa de la muestra es función del tamaño de partícula y de la varianza relativa del error fundamental.

Para construir este gráfico se consideró un CV =10% y un K exp = 4,22 (línea roja). Los datos usados para construir el protocolo del muestreo son los que se entregan en la siguiente tabla.

Para mayor información de la construcción e interpretación del diagrama de muestreo clásico, ver mi post denominado 

La teoría de Pierre Gy aplicada a los minerales

Referencias:

(1) P. Gy. "Sampling of Particulates Material. Theory and Practice". Ed. 1979. Ed. Elsevier Scientific Publishing Company.

(2) P. Gy. "Sampling of heterogeneous and dynamic material systems. Theories of heterogeneity, sampling and homogenizing". Ed 1992. Ed. Elsevier Scientific Publishing Company.

(3) Curso-taller: "Teoría y práctica del muestreo, basado en la teoría de Pierre Gy" de Mauricio Arancibia G.

Pincha aquí para saber más acerca de los cursos que se ofrecen en 2023: CURSOS ONLINE

Como determinar la línea de seguridad en un nomograma de muestreo de Pierre Gy

El siguiente artículo muestra como se determina la linea de seguridad de Pierre Gy en un diagrama de muestreo
.
Una vez creado el nomograma de muestreo, la pregunta que muchos se hacen es cómo se determina la línea de seguridad.

Para ello, partamos de la definición de desviación estándar relativa (DER en español, RSD en inglés) y que también se conoce como coeficiente de variación:

expresado en forma porcentual tenemos:

Ahora bien, si queremos incluir el término varianza relativa (que es como se expresa el error fundamental) en esta ecuación, podemos reescribir la expresión anterior de la siguiente manera:

Luego, despejamos la varianza relativa:

Por lo tanto,con esto obtenemos una ecuación que nos permite relacionar el CV% con la varianza del error fundamental.

Así para un CV = 10%, la varianza del error fundamental sería 0,01. Para un CV = 5%, la varianza del error fundamental sería 0,0025.

Ahora bien, que significa en la práctica aceptar un CV del 10%:
Para ello, necesitamos conocer la desviación estándar y la concentración media a considerar:

Así, para una concentración media de un metal del 2,0%:

s = 0,20%

Recordemos que el intervalo de probabilidad considerando un nivel de probabilidad del 95% se calcula de la siguiente manera:

Por lo tanto el intervalo para ese nivel de concentración y considerando ese nivel de probabilidad sería:

En conclusión, con una linea de seguridad fijada en 0,01 que equivale a un CV = 10%, para muestras con un nivel de concentración de metal del 2,0% se estarían aceptando dispersiones de +/- 0,40% considerando un nivel de probabilidad del 95%.

Ver mi otro artículo sobre la teoría de Pierre Gy: 

"La teoría de Pierre Gy aplicada a los minerales"

Pincha aquí para saber más acerca de los cursos que se ofrecen en 2023: CURSOS ONLINE

La teoría de Pierre Gy aplicada a los minerales

Han pasado más de 40 años de que Pierre M. Gy publicara su famoso libro “Sampling of particulates materials. Theory and Practice” (ed. 1979) y más de 50 años que estableciera su famosa expresión del error fundamental (1953). Sin embargo su legado sigue vigente hasta el día de hoy.

A continuación presento un breve resumen de su aplicación a la minería; 

En la moderna teoría del muestreo de P. Gy, se puede desprender que, existen dos principios que deben ser tomados siempre en consideración:

1.- “Que todos los constituyentes de interés del lote deben ser bien representados en la muestra"

2.- "Que en todo el proceso de muestreo se mantenga las características del lote original".

El primer principio está asociado al proceso de selección (a las operaciones selectivas), es decir aquella etapa donde se extrae una fracción a partir de un lote. Y están ligadas a ellas los siguientes errores; fundamental, segregación y/o agrupamiento, delimitación, extracción y ponderación.

El segundo principio, en cambio, está asociado a las operaciones no selectivas, es decir, a aquellas etapas del proceso donde no se extrae una fracción a partir del lote, como, por ejemplo; almacenamiento temporal, traslado, secado, conminución, homogenizado o mezclado, ensobrado, entre otros. En todas estas etapas sólo se puede producir el error de preparación.

Sin embargo, con el tiempo se han ido agregando otros errores contabilizando nueve hasta la fecha. Estos son:

A.- Heterogeneidad de corto plazo (EQ1)  

(asociados al proceso de selección, a excepción de EP)

1.- Efecto pepita (In situ Nugget); EN

2.- Fundamental; EF

3.- De Segregación y/o agrupamiento; ESG

4.- De Delimitación de los incrementos; ED

5.- De Extracción de los incrementos; EE

6.- De Ponderación; EW

7.- De Preparación; EP

B.- Heterogeneidad de largo plazo

(asociados al proceso de la planta)

8.- De fluctuación de la calidad (tendencias y desvíos); EQ2

9.- De fluctuación periódica (ciclos); EQ3

Nota.- El error analítico (EA) no se le considera parte del error de muestreo).

En síntesis el error total de muestreo (ET) se puede descomponer en los siguientes componentes :

ET =  [EN + EF + ESG + EQ2 + EQ3] + [ED + EE + EW] + EP

Los primeros cinco errores nunca podrán ser eliminados, pero si pueden ser minimizados, ya que los tres primeros forman parte inherente de la heterogeneidad con que se presentan los materiales en la naturaleza y los otros dos errores de largo alcance corresponden a la variabilidad que presenta el muestreo del material en la planta (en base a tiempo) o en la corteza terrestre (en base a masa), por ejemplo.

Los tres errores siguientes, ED, EE y EW es posible eliminarlos. Pero si no se aplican las prácticas del muestreo correcto, éstas pueden llegar a constituir fuentes importantes de sesgo. Los errores ED y EE están asociados a los dispositivos y a las técnicas de muestreo. En este sentido es importante utilizar la geometría correcta de estos dispositivos y la forma correcta como llevar a cabo el proceso de selección para evitar romper con los principios de equiprobabilidad y de integridad en el muestreo.

La geometría correcta de los dispositivos es la siguiente:     

a) Para lotes circulares, el dispositivo de muestreo debe ser radial

b) Para lotes lineales, el dispositivo de muestreo debe contemplar un paralelogramo o un rectángulo

Lo mismo aplica para las técnicas de muestreo.

Por último, en el caso del error de preparación, EP, las fuentes de sesgo que pueden ser completamente eliminadas al principio en el diseño correcto del sistema de muestreo y de preparación de muestras incluyen la pérdida de muestra, la contaminación de la muestra y la incorrecta extracción de los incrementos. Mientras, que las fuentes que pueden ser minimizadas pero no completamente eliminadas incluyen los cambios en el contenido de humedad, pérdida de polvo y degradación en el tamaño de partícula (para la determinación del tamaño).

Acerca del Error fundamental

El error fundamental corresponde a aquella variación producida por la heterogeneidad de constitución de las partículas o fragmentos, es decir, la variabilidad de una característica en particular entre partículas o fragmentos en cuanto a su composición química y/o mineralógica, forma, tamaño, densidad u otras propiedades.

La siguiente expresión corresponde a la varianza relativa del error fundamental:

donde:

S²(FE): varianza relativa del error fundamental;
M_s: Masa de la muestra (g);
M_L: Masa del lote (g);
d: Tamaño de partícula (cm³);
C: Constante de muestreo (g/cm³);
x̄: concentración del constituyente de interés.
s²: varianza del constituyente de interés.

La importancia de conocer el error fundamental para cada unidad geológica es que podemos estimar la masa mínima que necesitamos obtener en cada etapa de selección, y según esta ecuación esta masa mínima depende del tamaño de partícula y de la precisión que necesitamos para la toma de decisiones sin que introduzcamos sesgo en el proceso.

Para determinar la varianza del error fundamental, según esta ecuación, sólo necesitamos conocer la masa de la muestra, la masa del lote, el tamaño de partícula y la constante C.
Sin embargo, conocer la masa y el tamaño de partícula no reviste mayor dificultad en la práctica. Pero sí la constante C (que en realidad no es una constante para todos los estado de conminución).
Existen dos formas para determinar la constante C; una estimación "simplificada" o aproximada y la determinación experimental a través del Test de Heterogeneidad.
Para la estimación "simplificada" de la constante C necesitamos tener cierta información previa, ya sea de la literatura o de nuestro historial.
En este primer caso la constante C se descompone en 4 factores; factor de forma (f), el factor dependiente del rango de tamaño (g), el factor mineralógico (c) y el factor de liberación (l):

C = fcgl

En la determinación experimental mediante el Test de heterogeneidad, el material escogido para la prueba se somete a conminución después del secado y se pasa a través de un harnero vibratorio, donde se escoge una fracción para el test, que generalmente es de 1/2" a 1/4". De esa fracción, una cantidad exacta de diferentes fragmentos (n = 35 por ejemplo) deben ser escogidos al azar para conformar la muestra. Este procedimiento generalmente se repite unas 100 veces (100 muestras de x fragmentos cada uno), los cuales posteriormente se procesan como muestras independientes para la determinación de la característica de calidad.
La constante C obtenida en este test para esa fracción, luego se extrapola al resto de los estados de conminución, a través de una nueva constante que se denomina constante K para todos los estados de conminución.
El resultado final es la construcción de un gráfico log-log denominado "Nomograma" que permite visualizar el procedimiento más adecuado para las distintas etapas de selección sin que se introduzca sesgo en el proceso.
Cabe destacar, que la constante K se deriva de la siguiente expresión:

En esta expresión son constantes para todos los estados de conminución los siguientes términos: f, g, c, d_l.

donde d_l corresponde al diámetro de partícula donde se libera el mineral.
La constante C obtenida del test de heterogeneidad para esa fracción en particular nos sirve para determinar la constante K para todos los estados de conminución:

Las diferentes constantes C para cada estado de conminución, por lo tanto ahora la podemos obtener a partir de la expresión anterior:

Finalmente, con todos estos datos se construye el gráfico o nomograma respectivo a partir de la ecuación simplificada de la varianza relativa del error fundamental cuando la masa del lote (M_L) es mayor a 10 veces la masa de la muestra (M_s):

A partir de esta expresión se construye el nomograma, llevando la ecuación a escala logarítmica:

Aquí la pendiente de esta ecuación es -1.

En este diagrama de muestreo, las líneas diagonales representan los diferentes tamaños de partículas y la línea roja horizontal corresponde al límite de seguridad. Bajo esa línea, el proceso se encuentra en el lado seguro y sobre esa línea el proceso pasa a ubicarse en el lado inseguro.

Sobre cómo determinar la línea de seguridad del nomograma de Pierre Gy, visitar el siguiente post:
Línea de seguridad de Pierre Gy

Si quieres conocer el diagrama de muestreo preferido de Pierre Gy, visitar el siguiente post:
El diagrama de muestreo preferido de Pierre Gy

Más sobre la teoría de Pierre Gy en el siguiente post:

Como aplicar la teoría de Pierre Gy en la práctica 

(ARTÍCULO REVISADO Y CORREGIDO EN AGOSTO DE 2024)

Nota.- El siguiente artículo está basado en las siguientes fuentes:

(1) P. Gy. "Sampling of Particulates Material. Theory and Practice". Ed. 1979. Ed. Elsevier Scientific Publishing Company.

(2) P. Gy. "Sampling of heterogeneous and dynamic material systems. Theories of heterogeneity, sampling and homogenizing". Ed 1992. Ed. Elsevier Scientific Publishing Company.

(3) R.C.A. Minnitt*, P.M. Rice† and C. Spangenberg. "Part 1: Understanding the components of the fundamental sampling error: a key to good sampling practice". Ed. 2007. The Journal of The Southern African Institute of Mining and Metallurgy.
(4) ISO 3082: 2000. "Iron Ores - Sampling and sample preparation procedures".
(5) Curso de muestreo de minerales, de Mauricio Arancibia G,

Pincha aquí para saber más acerca de los cursos que se ofrecen en 2023: CURSOS ONLINE